2/92 cz I Praca domowa
Wśród prostokątów, których dwa wierzchołki należą do paraboli o równaniu y=(x+3)^2, zaś dwa pozostałe na prostej k:y=4, znajduje się taki, którego pole jest największe. Oblicz współrzędne wierzchołków tego prostokąta i jego pole.
Nie założyłem od razu, tak jak jest to zrobione w kryteriach, że x-owa punktu A leży po jeden ze stron osi symetrii paraboli (założyłem że dziedzina to (-5,-1). Przez co nie mogłem opuścić wartości bezwzględnej na długości odcinka jednego z boków prostokata. Czy coś takiego co napisałem w pkt4 (zazn. czerwona ramka) przeszłoby na maturze?

optymalizacja Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 2
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Jeśli problem jest symetryczny (tak jak tutaj) to na 100% można założyć, że rozwiązuje się zadanie po "jednej ze stron osi symetrii". Później należy napisać drugie rozwiązanie- symetryczne do niego.
- 5
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
@ADRYAN11
Mógłbyś dokończyć to zadanie, ponieważ wszystko co robisz jest dla mnie logiczne, ale jest inna dziedzina, znak w funkcji optymalizowanej i ostatecznie inna argument dla którego funkcja przyjmuje maximum.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Jasne, przesyłam rozwiazanie :) Na rysunku dołaczam wyjaśnienie 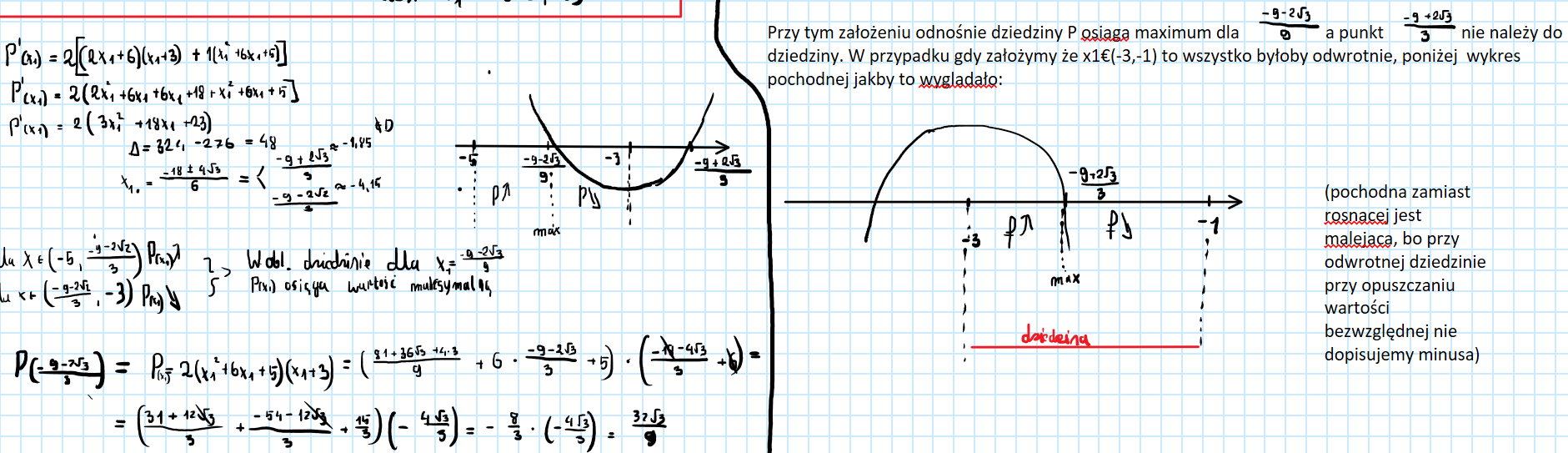
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Kliknęłam już napisz komentarz, a niestety nie dałam go rady usunąć.