1a/87
Dana jest parabola o równaniu y=ax^2. Udowodnij, że styczna do tej paraboli w punkcie (x0,y0) przecina oś OY w punkcie (0,-y0)
Co trzeba zrobić? Pochodną funkcji i co dalej?
matematyka geometria analityczna Dodaj post do ulubionych Poproś o pomoc
A umiałbyś b? Dana jest funkcja f(x)=x^3+3x^2+3,5x+7. Znajdź równania stycznych do funkcji f, które przecinają się z prostą y=1/3x+5 pod kątem 45.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Spróbuj sam:
1. Zapisz równanie stycznej do wykresu tej funkcji.
2. Skorzystaj ze wzoru z tablic na kąt między prostymi.
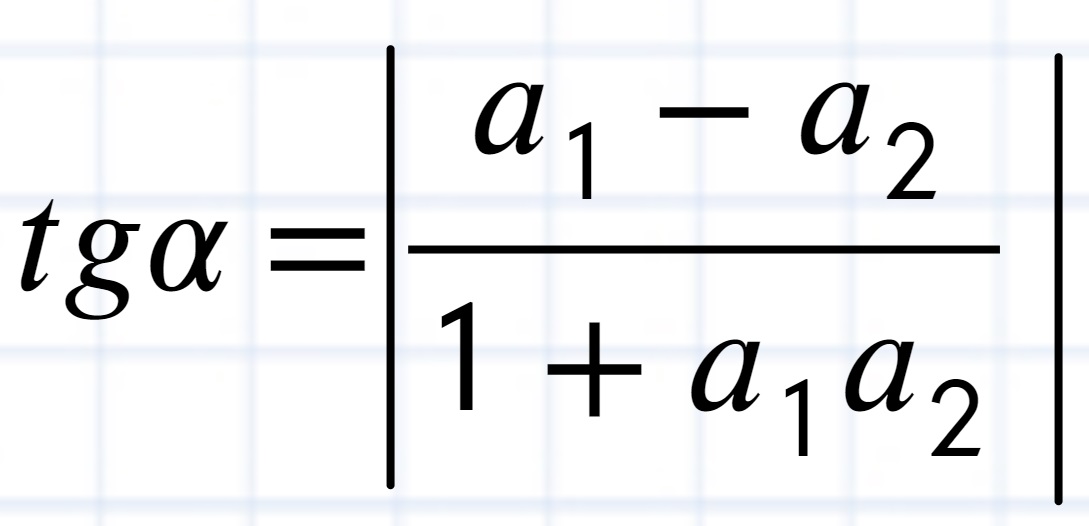
3. Wykorzystując ten wzór ułóż równanie.
4. Rozwiąż równanie i zapisz równanie tej stycznej.
W razie problemów pisz.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Jak zapisać równanie stycznej do tej funkcji? znam wzór y-f(x0)=f’(x0)x-x0).
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Zacznij od znalezienia współczynnika ,,a'' korzystając ze wzoru który ci podałem.
Wiesz że tg45 stopni to ,,1'' oraz wiesz że a1= 1/3 zatem wykorzystaj to. Wylicz współczynnik kierunkowy stycznej która ma tworzyć ten kąt.
W dalszym korku korzystając ze wzoru na współczynnik kierunkowy stycznej do wykresu wylicz x0 i po problemie.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
