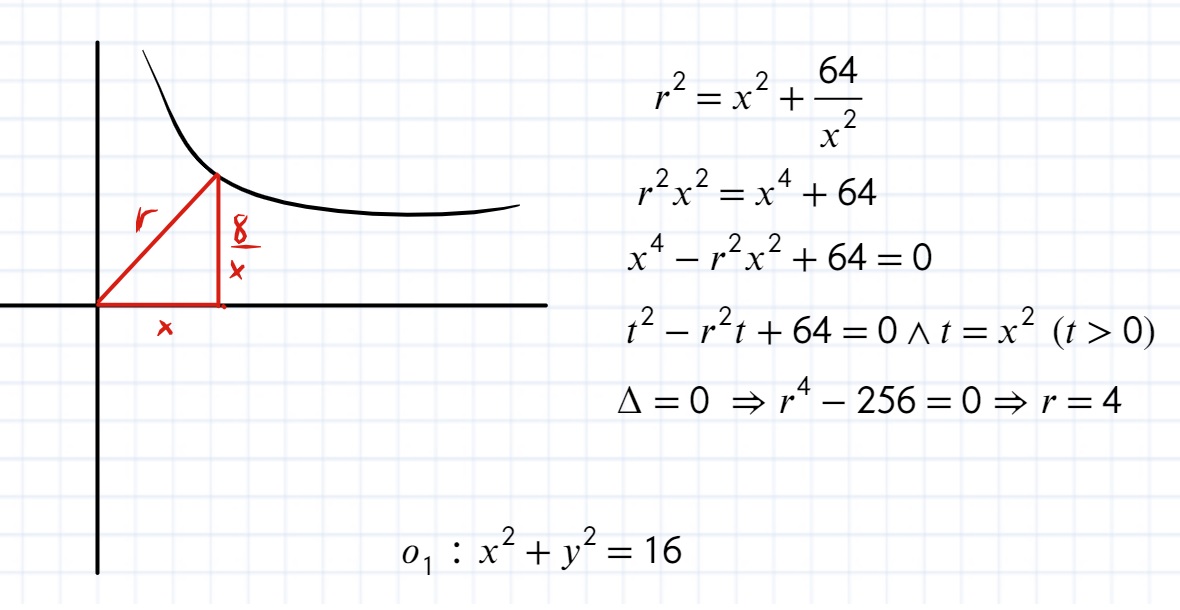Okrag styczny do funkcji homograficznej, zadanie nie wiem skad
Dana jest funkcja f(x) = 8/x . Napisz równanie okręgu o środku w początku układu współrzędnych, mającego dokładnie dwa punkty wspólne z wykresem funkcji f(x)=8/x
Czy zrobiłem to zadnie dobrze? Nie wiem czy wprowadzenie k jest w porzadku. No bo czuję to, że będzie ona prostopadła do osi symetrii funkcji homograficznej i że przejdzie przez punkty styczności ale trochę nie umiem tego uzasadnić.
Dodam jeszcze, że od punktu 3 niepotrzebnie skomplikowałem bo ten sam rezultat możnaby uzyskać obliczajac punkty przecięcia się prostej k i f(x)

geometria analityczna styczna do okręgu Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Odpowiadając na twoje pytanie, to tak. Te proste przecinają się pod kątem prostym, a wynika to z tego, że prosta ,,k'' jest również symetralną wykresu funkcji jak i układu okrąg funkcja, zatem proste y=-x i prosta y=x przecinają się pod kątem prostym.
Dla zobrazowania:
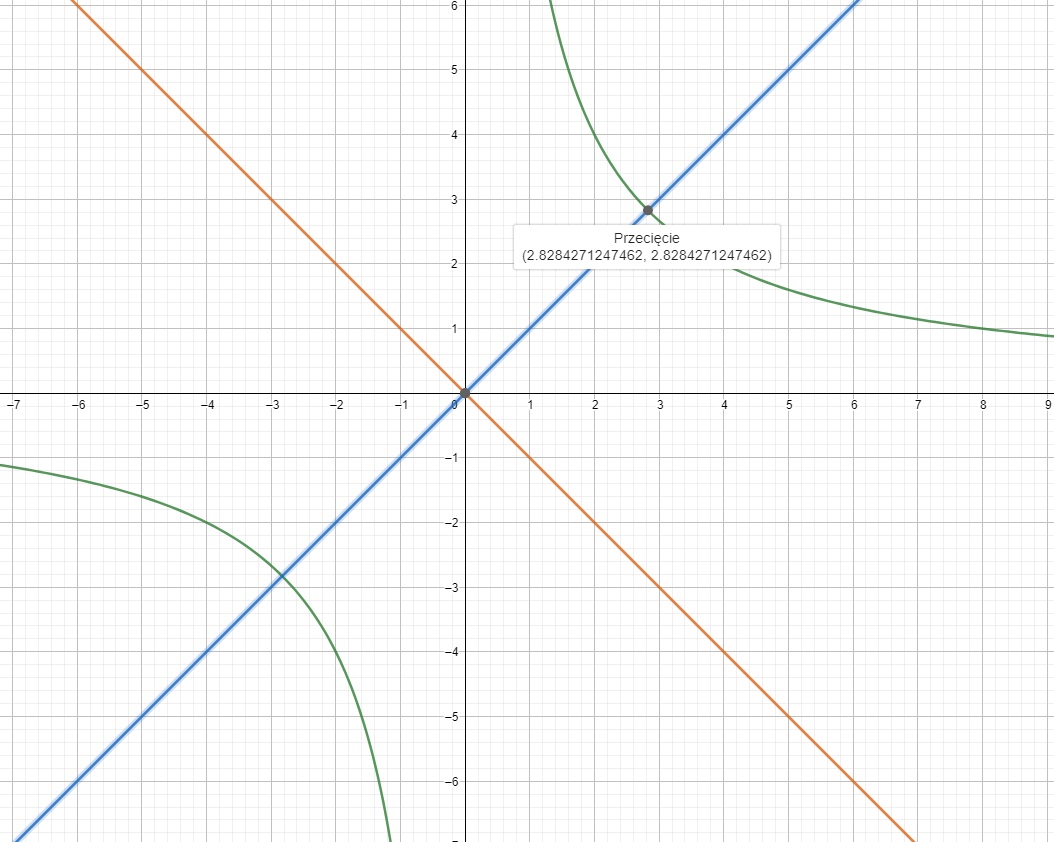
W skrócie twoje rozwiązanie jest poprawne: punkty się zgadzają, możesz w ten sposób rozwiązywać zadanie. Jeżeli chodzi o wyjaśnienie, to nawet nie jestem przekonany czy wymagałby ten zabieg jakiegoś specjalnego wyjaśnienia. Ewentualnie napisać, że punkty styczności będą leżeć na symetralnej układu okrąg - wykres.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Trochę skomplikowałeś to zadanie, wystarczy z pitagorasa wyliczyć promień.