... 517 wyśw. 17-03-2021 23:40

2d/74


Czy w poleceniu d) nie powinno być dopisane, że ,,2m'' należy do liczb całkowitych, a w poleceniu e) że m należy do całkowitych? Ponieważ w przeciwnym razie jest nieskończenie wiele takich parametrów ,,m'' dla których takie rozwiązania istnieją.

parametr wielomiany Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
Grzegorz.p7 17-03-2021 23:53

Nie. Zauważ że m nie musi być całkowite bo dla np m=0.5,współczynik dalej jest całkowity. 

Gdybyś dostał np m =3/4 to byś musiał takie rozwiązanie odrzucić bo gdy stosujesz twierdzenie o pierwiastkach wymiernych wszystkie wspolczyniki muszą być całkowite 

... 18-03-2021 00:04

Nie zrozumiałeś spójrz 

... 18-03-2021 00:05

Takich ,,m"-ów jest nieskończoność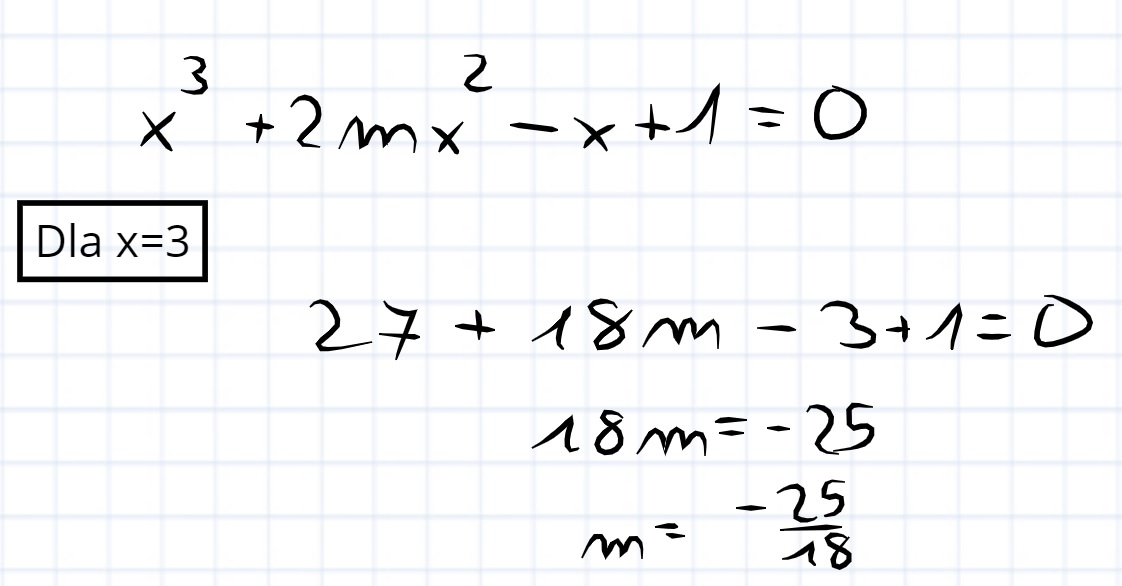 

Grzegorz.p7 18-03-2021 00:08
Dokładnie powinno być ze 2*m jest liczba całkowita. Inaczej jest tak jak mówisz 
... 18-03-2021 00:10

Dlaczego 2m? Chyba samo ,,m''

Grzegorz.p7 18-03-2021 00:11

Przed x^2 jest 2m czyli tak jak mówiłem gdy m wyjdzie np 0.5 to 2*0.5 =1 a to liczba całkowita 

... 18-03-2021 00:15

No tak w tym konkretnym przypadku 2m musi być całkowite.

Grzegorz.p7 18-03-2021 00:21

Autor zadania powinien napisać, że wspolczynniki są całkowite(lepiej niż samo m), bo inaczej tak jak napisałeś jest nieskończenie wiele rozwiązań. Pewnie Pan Jarosiński miał na myśli że są całkowite, ale nie dodał tego w zadaniu, z tego co pamiętam to w jakimś zadaniu możliwe ze w tym, jakieś rozwiązaniem się odrzucało bo współczynnik nie wyszedł całkowity. 

... 18-03-2021 00:25

Okej, super dzięki za rozwianie wątpliwości :)