arkusz 1 zadanie 6
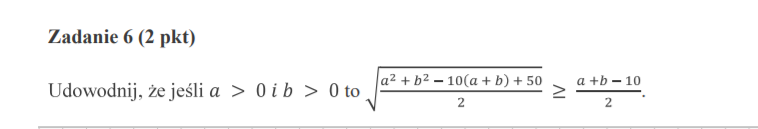
Dlaczego mozemy w tym zadaniu korzystać z zależności między średnimi, skoro składnikami, z których te średnie wyliczamy są liczby (a-5), (b-5) i wcale nie wiemy czy te składniki są dodatnie? Gdyby założenie w zadaniu brzmiało a i b są większe od 5, sytuacja wygladalaby zupelnie inaczej, poniewaz zarowno (a-5) jak i (b-5) byłyby na pewno dodatnie. Prosze o pomoc
nieujemnosc Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
okej czyli prawa strona może być ujemna?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
jesli prawa bedzie ujemna, a lewa dodatnia to zachodzi dodatnia > ujemna
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
@Grzegorz.p7
A co w sytuacji gdy: (a-5) będzie liczbą ujemną a (b-5) będzie liczbą dodatnią taką, że (b-5)+(a-5)>0 ?
Wtedy nie można skorzystać z nierówności między średnimi a z drugiej strony prawa strona jest dodatnia więc nie można od razu zamknąć dowodu.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
a to nie działa tak, ze to założenie a,b > 0, jest po to zeby wlasnie pod pierwiastkiem byla liczba dodatnia, bo inaczej mamy sprzeczne równanie? w tym wypadku na pewno jest wiec, nawet w takim przypadku jak mowisz mozemy skorzystac z nierownosci miedzy srednimi?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
jednak raczej to co napisałem komenatrz wyzej jest nieprawda

- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
juz sie sam zagubiłem, ale patrzac na to kolejny raz to skoro prawa strona bedzie dodatnia i lewa dodatnia to i tak wynika z nierownosci miedzy srednimi ze ta nierownosc jest prawdziwa. bo tak jak na zdj co wysłałem wyzej, wszytko zostaje tak samo a nie wkladamy tam modułu w s srednia arytemtyczna
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych

Oczywiście jeszcze przypadek gdy się zerują (...)
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Moim zdaniem w ten sposób powinno być to zrobione, chyba, że nie rozumiem jak w pełni działają nierówności miedzy średnimi ( istnieje taka możliwość haha), natomiast biorąc pod uwagę fakt który przekazał nam Pan na lekcji (że, zmienne muszą być dodatnie) to w mojej opinii to zadanie wymaga szerszego komentarza niż : z nierówności między średnimi.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Wydaje mi się, że rozumiem co masz na myśli i jestem w stanie się z tobą zgodzić, natomiast w takim wypadku, czy da się zgeneralizować sytuacje w których wykorzystujemy nierówności między średnimi mimo iż zmienne są ujemne?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
wydaje mi iż nie chodzi o te zmienne czy są dodatnie czy ujemne,a tylko o to żeby średnia(arytmetyczna,geometryczna itd.) była dodatnia. Ale nie chce o tym mówić więcej o tym bo nie jestem przekonany tego wszystkiego na 100%, tak jak pisałem wyżej. I myślę ze najrozsądniej będzie jak poproszę Pana Jarosińskiego, żeby tutaj spojrzał
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Dzięki za poświęcenie czasu :)
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
W tym zadaniu kryteria są troszkę niedoprecyzowane.
Przedstawione rozwiązanie rzeczywiście dotyczy zbioru zmiennych a i b większych od 5.
Dla liczb z przedziału (0 ; 5> strona lewa: L >=0, P <0, ckd.
- 4
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A co w sytuacji gdy jedna liczba jest z jednego przedziału a druga z drugiego, taką sytuację należy rozważyć?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Słuszna uwaga- należy jeszcze rozpatrzyć przypadek gdy jedna liczba jest z jednego przedziału a druga z drugiego. Wtedy gdy prawa strona jest ujemna to nierówność zachodzi zawsze. A gdy prawa strona jest dodatnia, to można podnieść do kwadratu i udowodnić, że zachodzi zawsze:
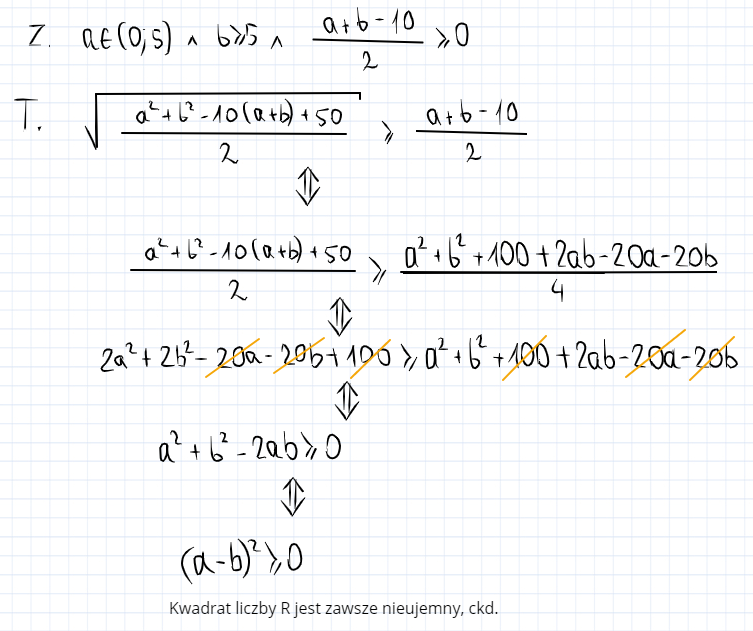
- 3
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
W nierównościach pomiędzy średnimi dodatnie mają być zmienne:
https://forum.szkolamaturzystow.pl/wpis/1616329931-arkusz-1-zadanie-6?notif=komentarzdodany
- 3
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
ale (a-5)^2 + (b-5), sa w kwadracie, a wiec sa na pewno nieujmne, stad to co jest pod pierwiastkiem jest na pewno nieujmne, wiec mozna skorzystac z nierownosci miedzy srednimi