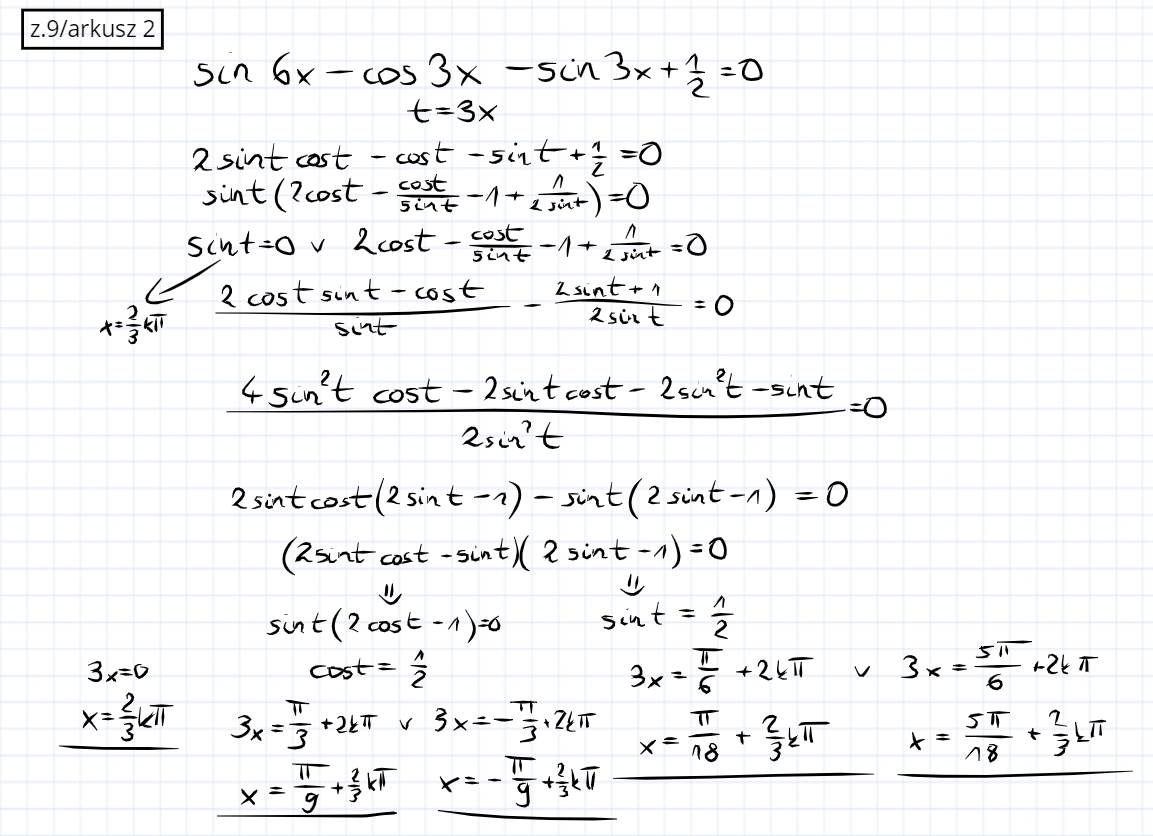robertkubica 1233 wyśw.
21-03-2021 18:35
Arkusz II zadanie 9
Wyznacz pierwiastki równania: sin(6x) - cos(3x) - sin(3x) + (1/2) = 0
Wiem, że równanie można zapisać w postaci 2sin(3x)cos(3x) - cos(3x) - sin(3x) + 1/2 . Jak pogrupować to wyrażenie żeby powstała postać iloczynowa? Bo nie wiem jakim sposobem to równanie można zapisać w postaci (2cos3x-1)(sin3x-(1/2))
równanie trygonometria Dodaj post do ulubionych Poproś o pomoc
Kliknij tutaj, aby dodać nowy komentarz.
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
Emil
22-03-2021 00:33
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Grzegorz.p7
23-03-2021 12:41
Emil
23-03-2021 15:34
To ma sens, dzięki Grzegorz za poprawkę ; )
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
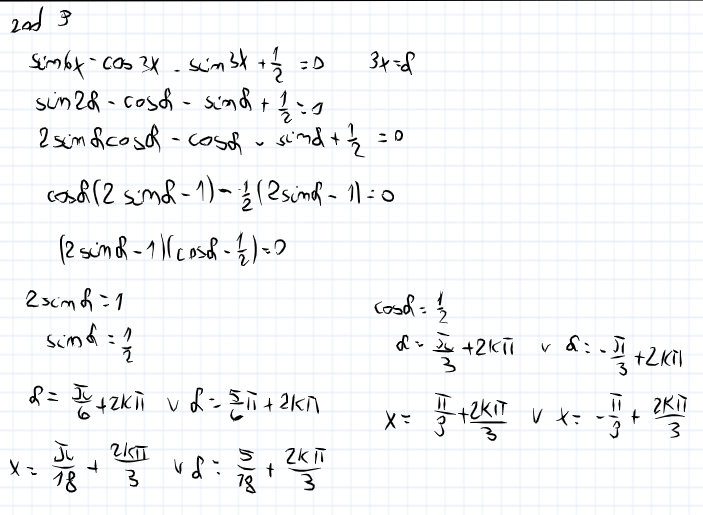
Po wymnożeniu tej postaci iloczynowej otrzymamy: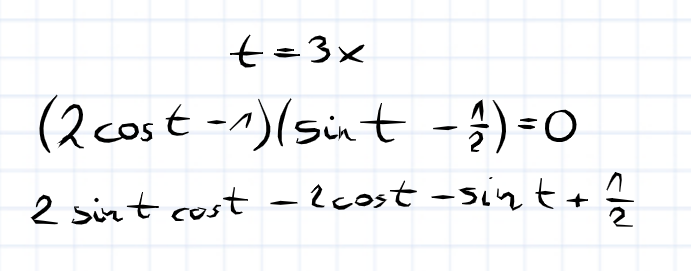
więc moim zdaniem w tym równaniu brakuje tej "2" przy cos(t), aby otrzymać taką postać.
Obliczyłem to zadanie wyciągając przed nawias sin(t), wyniki wyszły te same, zaś do nich dołączył jeszcze x=2/3kPI