7.85 c Kłaczkow

To jest do zrobienia, tylko pytanie po co? Mogę ci rozpisać początek, ale to jest porównywalne do rozpisywania stu cyfrowych liczb, da się to zrobić ale szkoda czasu. To jest zadanie stricte pod zdarzenie przeciwne i czasami nie da się inaczej.

Proszę, sprostałem :)

Właśnie o to rozwiązanie mi chodziło, bo nie wiedziałem, gdzie popełniłem błąd. Dzięki wielkie :)

Ja tutaj już nie rozumiem na etapie drugiego przypadku: (13 po 3)*4*(39 po 1)*3 tak powinno być moim zdaniem bo najpierw wybieramy 3 karty tego samego koloru i są 4 kolory, potem dobieramy 1 w innym kolorze (zostały 3 kolory) spośród 39 pozostałych kart. Moim zdaniem jeśli nie przemnożymy tu razy 3 to niektóre sposoby z tego przypadku powtórzą się już z przypadkiem pierwszym.

@Artur, mnożąc przypadki przez 3 zwiększasz ilość możliwości. 

Któryvh przypadków twoim zdaniem brakuje?

Chociażby drugi przypadek, który napisał "...": Moim zdaniem właśnie brakuje tam przemnożenia przez 3, bo ostatnia karta właśnie nie powinna być dowolna tylko w kolorze innym niż 3 pozostałe.

Mam na myśli abyś zapisał konkretny przypadek którego brakuje. W rozwiązaniu ... wszystko się zgadza.

No to brakuje mi właśnie tych wyborów kolorów poszczególnie do każdego przypadku tak jak napisałem o tym przemnożeniu przez 3 i zastanawiam się czemu tego nie można właśnie przemnożyć.

Przecież jest uwzględniony każdy kolor. W samym podpunkcie drugim jest napisane: "na koniec *4 ponieważ każdy ponieważ trzema kratami może być każdy z 4 kolorów"

No ale wtedy czwartą kartę już można wybrać tylko na 3 sposoby, aby nie była ona w kolorze trzech pozostałych.

Ten kolor dobierze się "samodzielnie" jeżeli wybierasz pierw spośród 13 kart danego koloru, a następnie spośród pozostałych kart 39 to już nie ma tam wybranego koloru (pozostaje tylko 3)

To jest niezbyt intuicyjne w takim razie. Skoro mnożymy razy 4 liczbę wyborów trzech kart tego samego koloru to analogicznie powinno być razy 3 dla ostatniej karty. Bo nie rozumiem w jaki sposób to nie przemnożenie razy na końcu sprawia, że jesteśmy pewni tego, że ostatnia karta jest innego koloru niż 3 pozostałe.

Pełne wyjaśnienie dla ciebie:

Chyba zaczynam to rozumieć. Czyli gdy wybierzemy kolor dla kart w tym samym kolorze to dla pozostałych kart dobiera się on jakby automatycznie. A dlaczego mam teraz błąd w przypadku 3?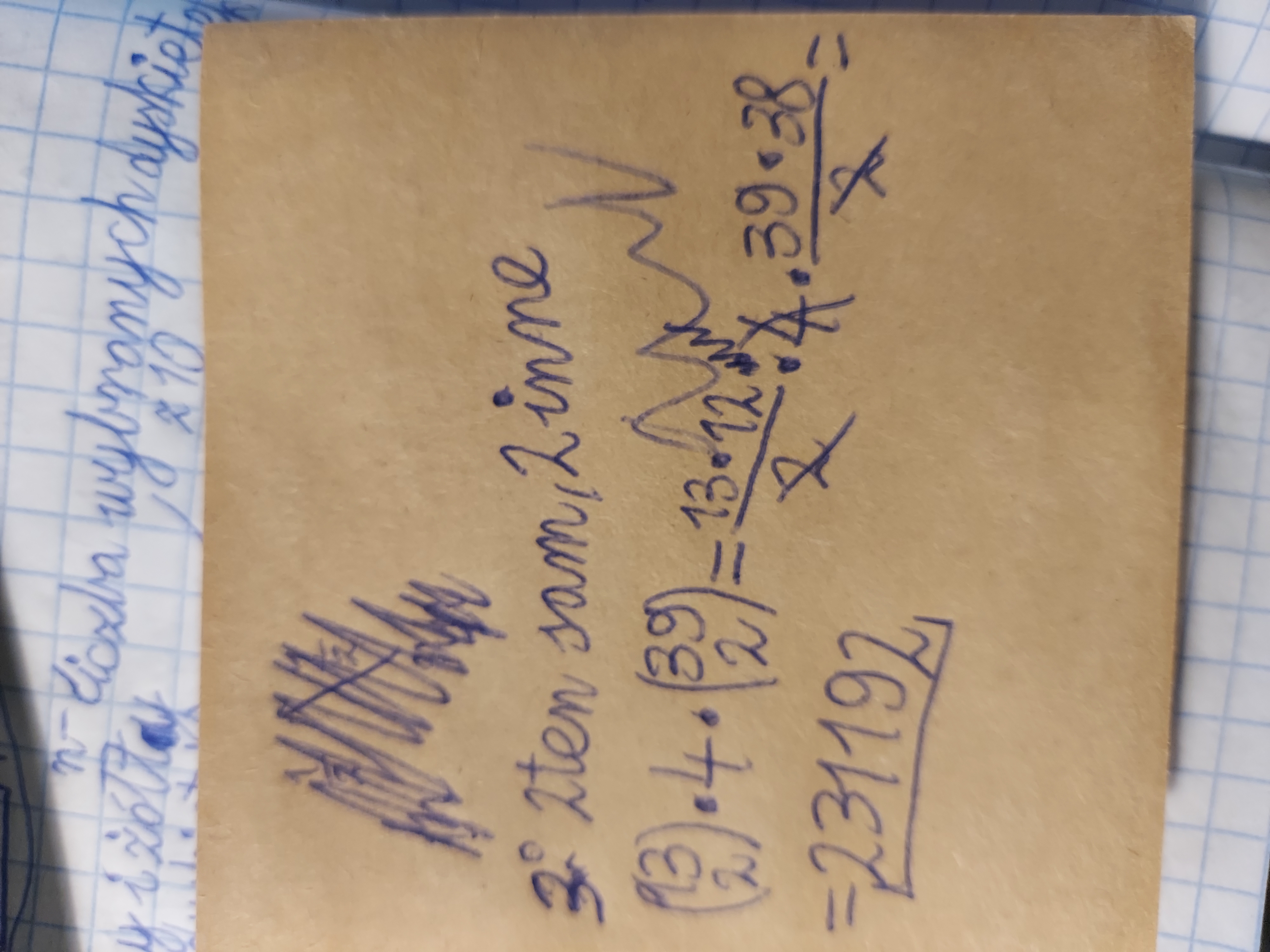

Od lewej: wybór kart ten sam kolor*wybór koloru*wybór kart pozostałych?

Ponieważ zliczasz np przypadek: 
2 kiery  pierw i później 2 karo

oraz 

2 karo i później 2 kier

A w jaki sposób tego uniknąć?

Obliczyć to tak jak zrobił to @...