Arkusz2/7
Suma pierwszych sześciu wyrazów ciągu geometrycznego rosnącego wynosi 728, a suma wyrazów; trzeciego i drugiego tego ciągu wynosi 24. Oblicz ile wynosi suma czwartego i szóstego wyrazu tego ciągu.
Więc zapisałem wszystko z oznaczeniami dla a1 i q i z tej sumy sześciu wyrazów wyłączyłem a1 i wyszło a1(1+q1+q2+q3+q4+q5)=728. Rozumiem, że to co w nawiasie to ciąg i można go zapisać jako sumę, ale nie rozumiem dlaczego w odpowiedziach ona wynosi 1-q^2/1-q. Wytłumaczyłby ktoś?
matematyka matura ciągi Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Zgodnie ze wzorem na sumę początkowych n wyrazów ciągu geo to powinno. A wyszło ci jak zrobiłeś q^6?
Bo ja się zakopalem w potegach ;|
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Właśnie też się pogubiłem. Ma ktoś to zadanie zrobione?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
q=3 bo dla q=3 ten wielomian sie zeruje

- 3
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Macie rację, w tym zadaniu wkradła się literówka do kryteriów. Powinno być: 1-q^6/1-q. A poprawne rozwiązanie przedstawił @Grzegorz.p7
- 6
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Przekształciłem to równanie końcowe do takiej postaci.
Z niej już widać, że rozwiązaniem jest q=3, natomiast jak udowodnić, że z podkreślonego nawiasu nie uzyskamy pożądanego q? Bo patrząc na geogebrę widać, że z tego nawiasu będzie jeszcze jeden pierwiastek dodatni niewymierny.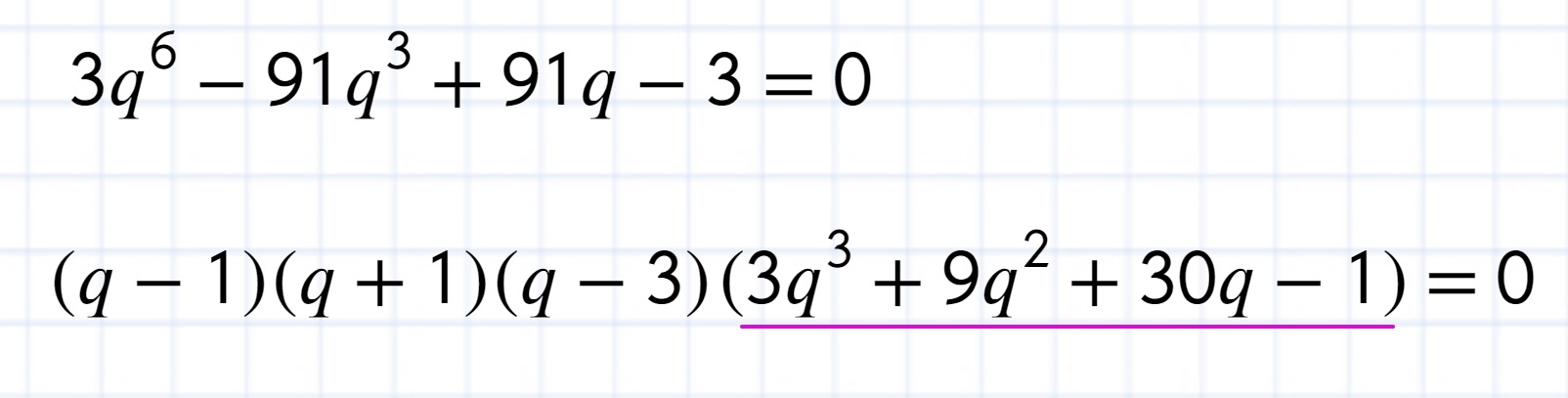
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Można go przybliżyć lub pokazać, że jest ono mniejsze od 1 (a ciąg jest rosnący, zatem to rozwiązanie nas nie interesuje)
- 2
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Dokładnie. A potem jeśli potrzebujemy dokładniejszego przybliżenia to liczymy wartości w połowie danego przedziału. Czyli jeśli podejrzewamy, że miejsce zerowe jest z przedziału (0 ; 1). To liczymy f(1/2). Jeśli po obliczeniu się okaże, że miejsce zerowe jest z przedziału (0; 1/2) to liczymy f(1/4) itd. aż osiągamy przybliżenie które nas satysfakcjonuje
- 3
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych

Skoro wiemy, że ten ciąg ma 6 wyrazów to nie powinno być 1-q^6/1-q?