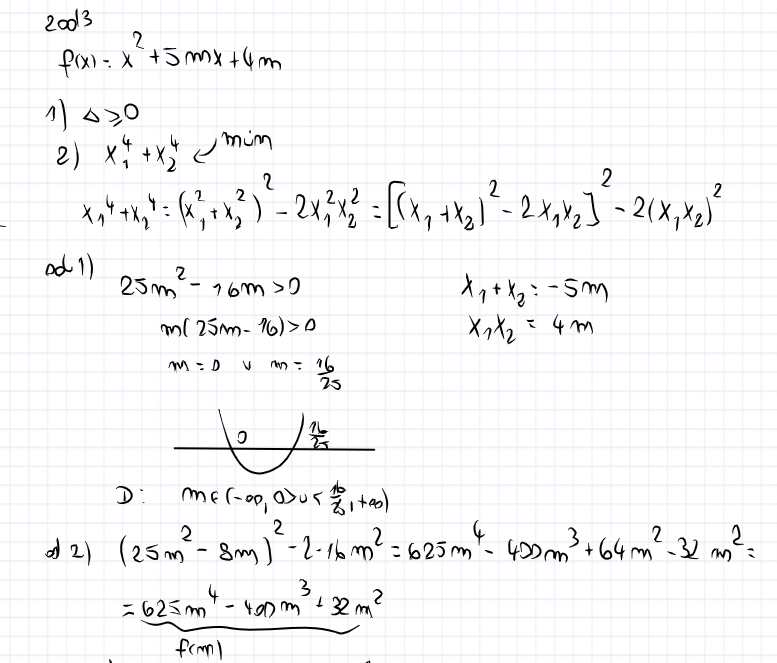Zad 3/93 cz.II
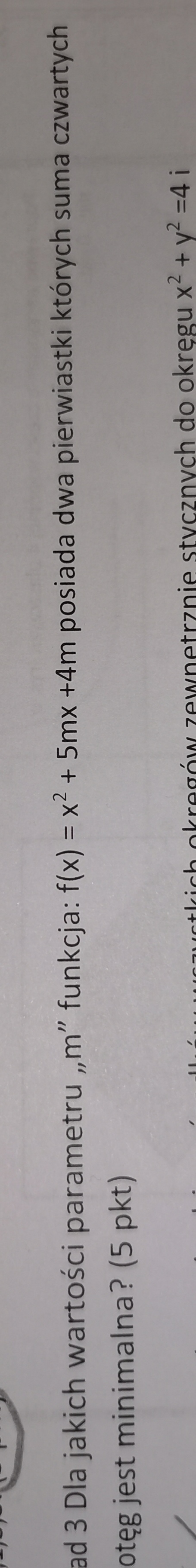
Hej mógłby mi ktoś rozpisać to zadanie do uzyskania funkcji optymalizowanej?
Matematyka Dodaj post do ulubionych Poproś o pomoc
A mógłby ktoś jeszcze powiedzieć dlaczego w tym zadaniu musimy obliczyć wartość krańcową S(16/25)?
Przeciez z wykresu zmienności funkcji widzimy że nie osiąga dla tego argumentu minimum.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Owszem, funkcja nie osiąga minimum dla m=16/25. Ale po zbadaniu pochodnej (wykres 1) znamy tylko monotoniczność tej funkcji oraz jej ekstrema i nic ponad to. Zatem to za mało, aby stwierdzić, gdzie funkcja w wyznaczonej dziedzinie będzie osiągała wartość najmniejszą. Zauważ, że gdyby wartość tej funkcji w drugim minimum (nienależącym do dziedziny) osiągała wartość mniejszą od pierwszego minimum, to możliwe jest, aby wartość funkcji w m=16/25 była mniejsza od wartości w pierwszym minimum (wykres 2). Zatem, aby przekonać, jak jest naprawdę, liczymy wartości funkcji w ekstremach i na krańcach dziedziny, czyli m=0 i m=16/25. Wychodzi, że jednak wartość w pierwszym ekstremum jest mniejsza od wartości w drugim ekstremum (wykres 3), zatem mamy minimalną wartość funkcji w naszej dziedzinie.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych