ADRYAN11 1012 wyśw. 25-03-2021 22:33

Arkusz 5 zadanie 8

Wyznacz te wartości parametru m dla których równanie |(x-2)/(x+2)| - 2 -m =0 z niewiadoma x ma dokładnie jedno rozwiazanie. 

Wyszły mi dwie możliwości: m=-2 v m=-1. W odpowiedzi jest tylko ta pierwsza. Dla +-niesk. funkcja daży do wartości -1 ponadto f(0)=-1 . Czy zatem m=-1 nie spełnia też warunków zadania? 
Piszac funkcja mam na myśli: f(x) = |(x-2)/(x+2)| - 2  


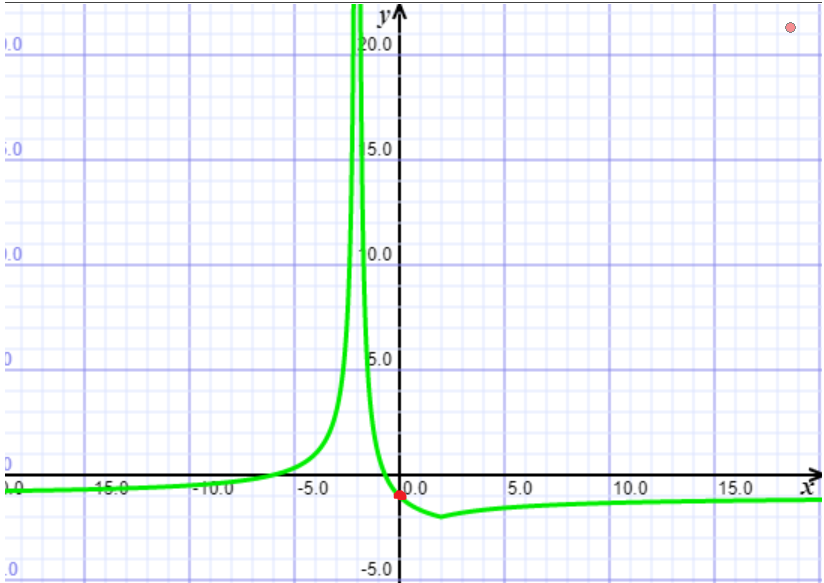
rysowanie wykresu Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
Grzegorz.p7 25-03-2021 22:37

zobacz tutaj, w -1 jest asymptota pozioma, wiec nie(koncowa funkcja to ta fioletowa i ta co styka sie z tą błękitną linią(kolor mi sie nie zmienil na fioletowy))


ADRYAN11 26-03-2021 12:44

No tak, ale właśnie o to mi chodzi. Mamy asymptotę, więc funkcja  gdy daży do niekończoności nigdy nie osiaganie wartości -1. Ale przecież jednocześnie osiaga ja w punkcie (0,-1). Popatrz na mój wykres: (zaznaczyłem na fioletowo oba punkty)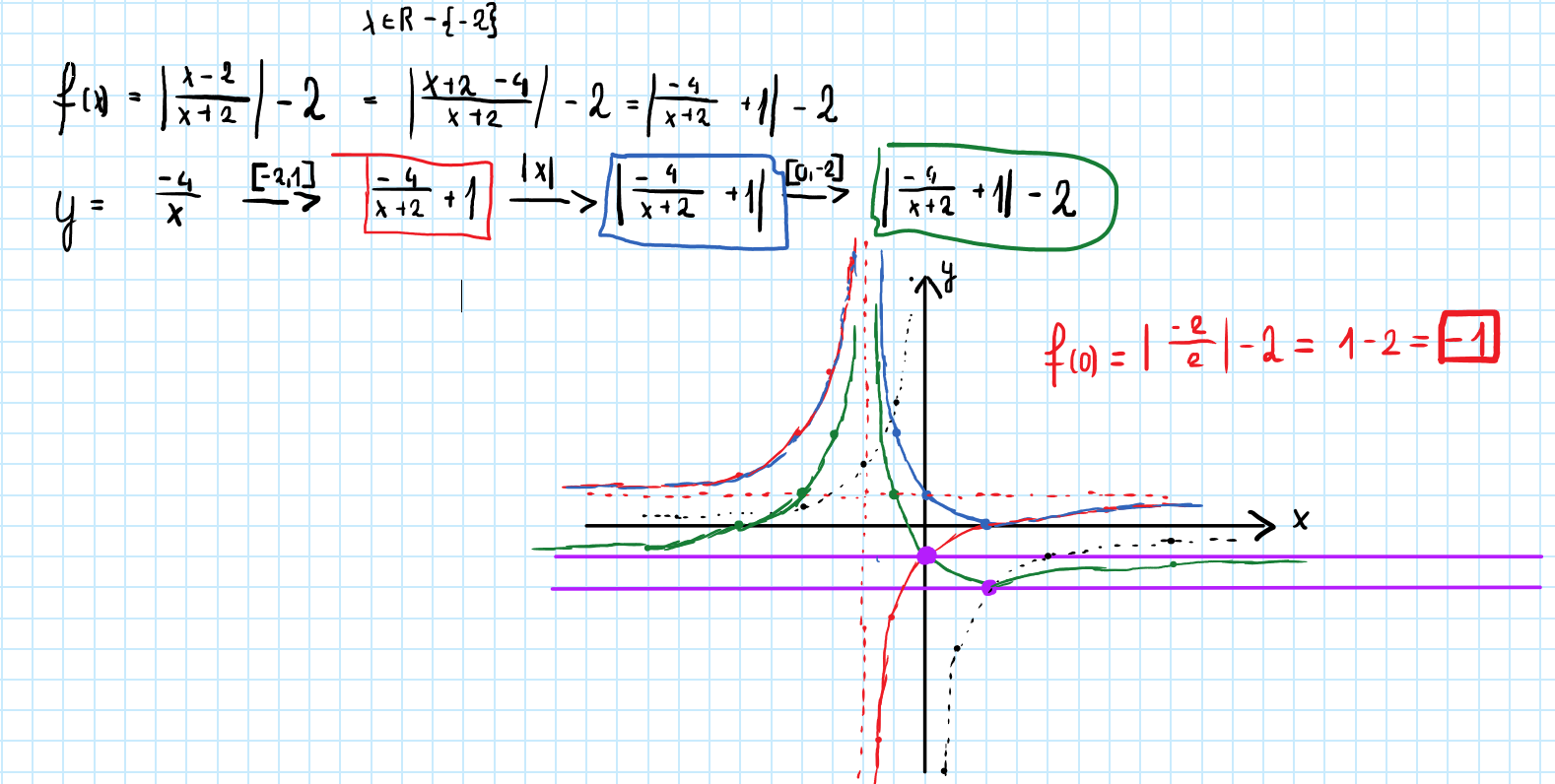

Grzegorz.p7 26-03-2021 12:47

rzeczywiście, a wiec by wychodzilo ze m= -2 i -1