Arkusz 5 zadanie 13
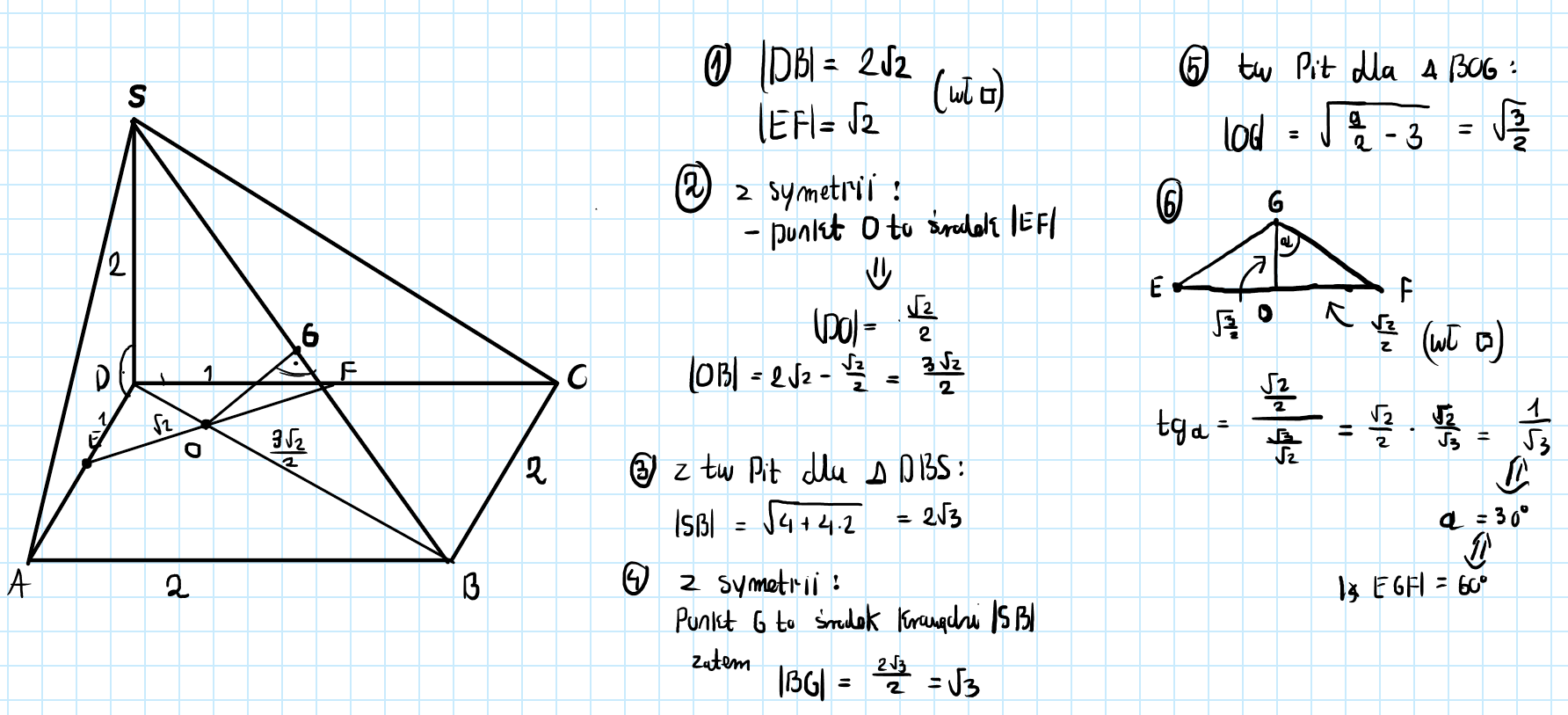
W ostrosłupie AABCDS podstawa jest kwadrat ABCD o boku 2. Krawędź boczna DS jest wysokościa tego ostrosłupa, a jej długość jest równa długości krawędzdi podstawy. Punkty E i F sa odpowiednio środkami krawędzi AD i CD. Płaszczyzna przechodzaca przez punkty E i F jest prostopadła do krawędzi bocznej BS i przecina tę krawędź w punkcie G. Oblicz miarę kta EGF i długość boku
Na zajęciach ze stereometrii mówiliśmy, że jeśli nie wiemy jak coś udowodnić to powołanie się na symetrie powinno wystarczyć. Czy zatem takie rozwiazanie było by zaliczone - głównie chodzi mi o podpunkt 4
stereometria ostrosłup symetria Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Myślałem o płaszczyźnie EFG. Doszedłem do wniosku że jeśli punkty E i F sa to środki boków, to prosta zawierajaca odległość z punktu O do przekatnej będzie dzielić ta przekatna w połowie. Nie wiem dlaczego, zwyczajnie uznałem że tak musi być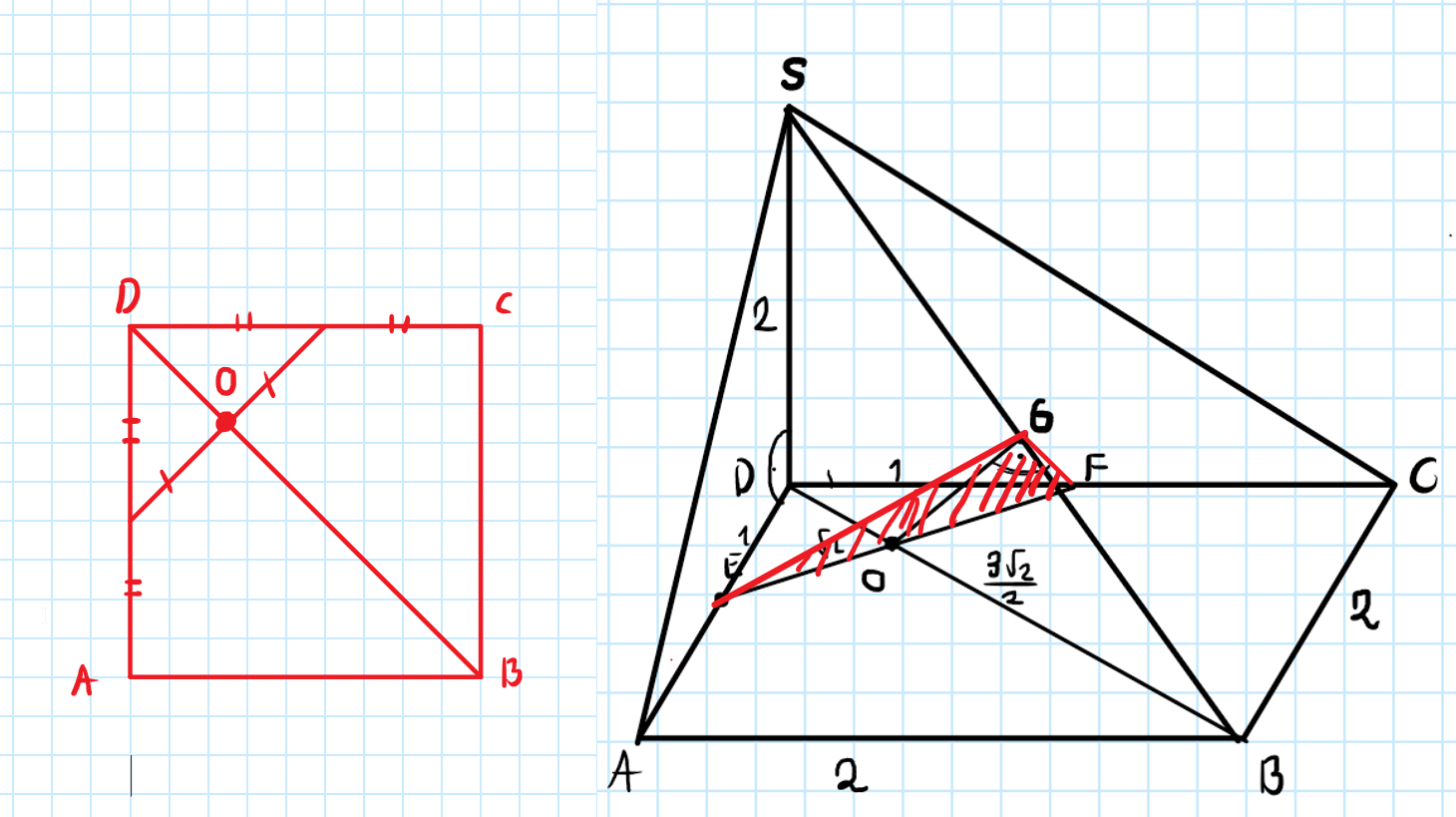
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Można tak zrobić zawsze gdy jest to prawda (ale nie potrafisz jej udowodnić). A jaką symetrię miałbyś tutaj na myśli?