Wzory Viete'a arkusze.
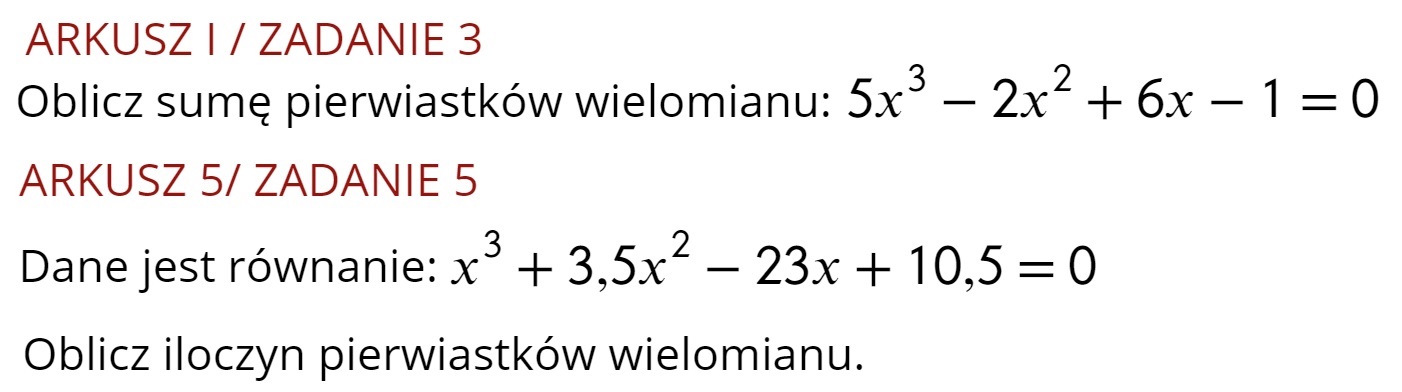
W obydwu zadaniach działa sposób z wykorzystaniem wzorów Viete'a dla wielomianu 3 stopnia.
Natomiast czy ten sposób jest zawsze poprawny bez żadnego sprawdzenia czy wielomian na pewno ma 3 pierwiastki?
Bo przykładowo biorąc pierwsze równanie z zadania 3 arkusza 1.
Wielomian z lewej strony ma jeden pierwiastek rzeczywisty równy około 0,17 natomiast jeżeli skorzystamy z wzorów Viete'a to otrzymamy wynik taki jak w kryteriach czyli 0,2.
Wiem dlaczego tak się dzieje (wzory Viete'a zliczają również pierwiastki zespolone).
Dlatego moje pytania są takie:
-Czy zawsze możemy w takich zadaniach w których polecenie to ,,oblicz sumę pierwiastków wielomianu" albo ,,oblicz iloczyn pierwiastków wielomianu" zastosować wzory Viete'a nie zważając na to ile rzeczywistych pierwiastków ma wielomian 3 stopnia?
Bardzo proszę o komentarz jeżeli jest się przekonanym swojej odpowiedzi w 100%.
wzory Viete'a wykorzystanie wzorów pierwiastki wielomianu Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tak tylko z tego co wiem poziom licealny nie obejmuje liczb zespolonych, idąc w tą stronę każdy wielomian ,,n'' stopnia ma ,,n'' rozwiązań.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tak, nie obejmuje, ale nie trzeba tych pierwiastków wyliczać, z wzorów vieta wychodzi suma i iloczyn.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
@drzazgusia w pytaniu było
"Wielomian z lewej strony ma jeden pierwiastek rzeczywisty równy około 0,17 natomiast jeżeli skorzystamy z wzorów Viete'a to otrzymamy wynik taki jak w kryteriach czyli 0,2."
I stąd pytanie dlaczego mozemy i czy powiniśmy uzywac takiej metody skoro pierwiastkiem jest 0.17, a przez iloczyn wychodzi 0.2
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Witam, jeżeli wielomian jest 3 stopnia to zawsze ma chociaż jeden pierwiastek rzeczywisty, nie musi ich mieć wcale 3 ale jeden napewno będzie miał i używając wzorów vieta wyjdzie ile ich jest. Tak można używać tych wzorów. Pozdrawiam.