Zadanie domowe nr 26, Zadanie 7.3/str 359

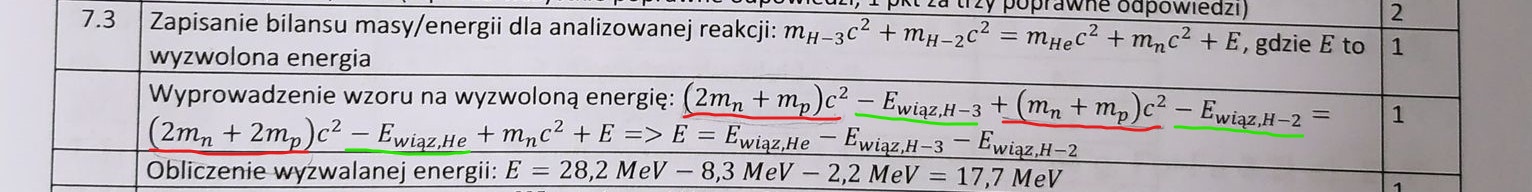
Z czego wynika wyprowadzenie wzoru na energię wyzwoloną?
Zapisałem bilans energii, ale dlaczego w kolejnym kroku odejmujemy od energii wiązania z bilansu (kolor czerwony?), inna energię wiązania (kolor zielony)? Dlaczego wolny neutron posiada energię wiązania, chociaż jest "samotny"?
fizyka Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Dobrze, natomiast w jaki sposób trzeba wyprowadzić drugi wzór?
Rozumiem, czym są czerwone i zielone wyrazy, ale nie wiem dlaczego od energii spoczynkowej odejmujemy energię wiązania.
Czy energia spoczynkowa zawiera w sobie energię wiązania?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Bierze się to z bilansu masy jądra, który przedstawialiśmy na zajęciach. Wiemy, że dla jądra składającego się z N neutronów i Z protonów mamy następujące równanie: N*mn + Z*mp = Mjądra + deltaM (deltaM to deficyt masy). Toteż np. dla jądra helu-4 dostajemy: 2*mn + 2*mp = MHe + deltaMHe. Stąd możemy wyrazić samą masę jądra: MHe = 2*mn + 2*mp - deltaMHe. Jeśli teraz przemnożymy to obustronnie przez c^2, to dostaniemy: MHe*c^2 = (2*mn + 2*mp)*c^2 - deltaMHe*c^2, a wyrażenie deltaMHe*c^2 to właśnie energia wiązania jądra helu (bo z definicji jest to iloczyn deficytu masy i c^2). W związku z tym mamy: MHe*c^2 = (2*mn + 2*mp)*c^2 - EwiązHe. To samo można zapisać dla jąder wodoru po lewej stronie reakcji i stąd bierze się owo równanie.
Co do pytania czy energia spoczynkowa zawiera w sobie energię wiązania, to należałoby je trochę doprecyzować, ale odpowiedź brzmi w zasadzie następująco: energia spoczynkowa jądra to suma energii spoczynkowych składników jądra pomniejszona o energię wiązania (pokazuje to np. wyprowadzony powyżej wzór MHe*c^2 = (2*mn + 2*mp)*c^2 - EwiązHe). Więc energia wiązania tam niejako siedzi, ale jest ona odejmowana.
- 3
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Teraz jest wszystko jasne, dziękuję za pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych