2016.C10.3
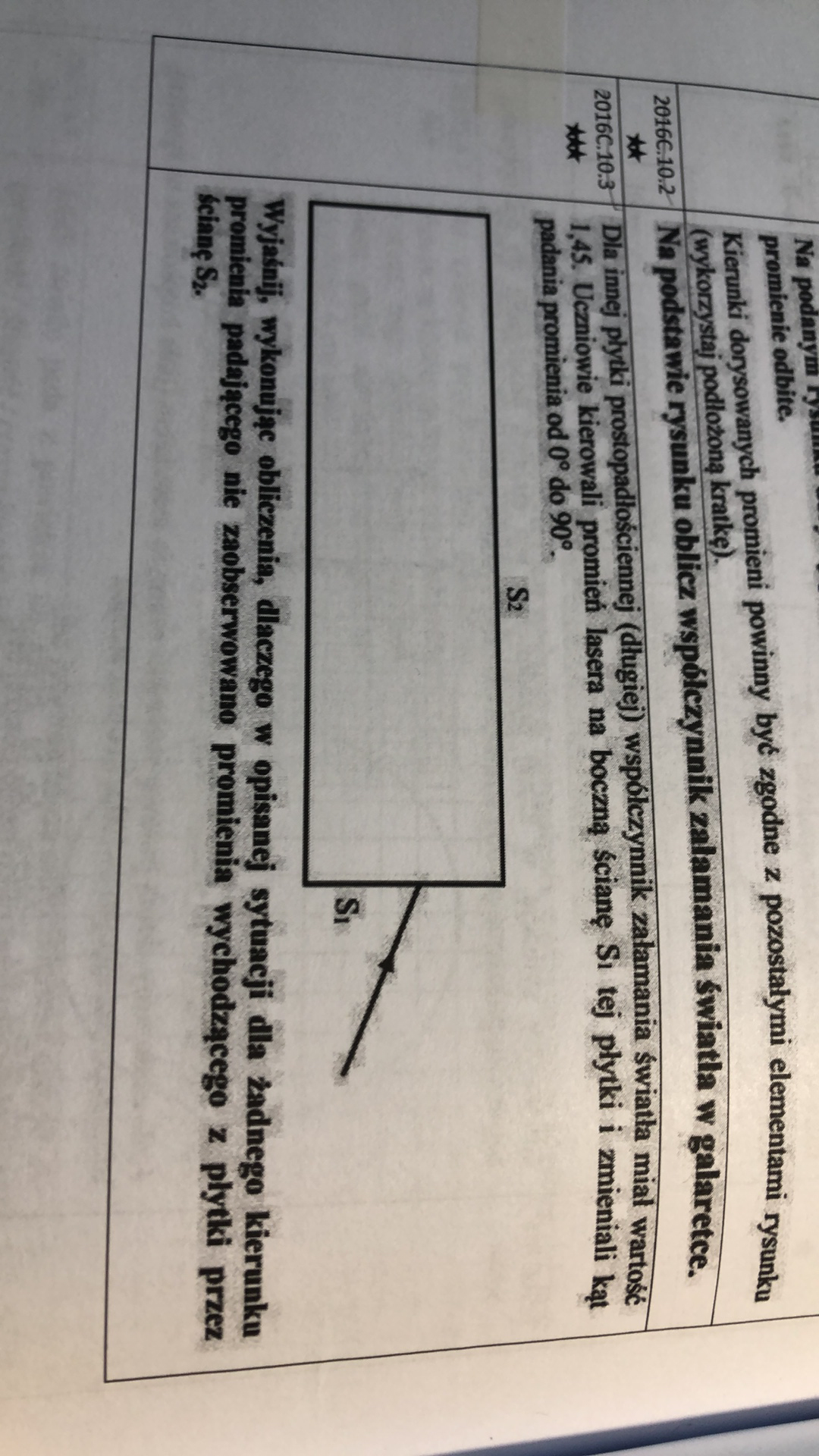
Znalazłam rozwiązanie tylko w ZZ na stronie CKE, ale nic z tego nie rozumiem udało obliczyć mi się kąt graniczny, a dalej nie wiem jak to udowodnić.
optyka fizyka Dodaj post do ulubionych Poproś o pomoc
- 3
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A w którym miejscu jest kąt alfa i beta? Bo jakoś mi się to miesza. Czy alfa jest przed przejściem S2?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Według oznaczeń z tego poprzedniego mojego komentarza alfa to kąt padania wiązki światła na pierwszą ściankę S1 (przy przejściu powietrze-szkło), natomiast kąt beta to kąt załamania dla tego właśnie przejścia.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
No to w takim razie ja może mam błąd w rozumowaniu, bo sinus kąta granicznego to stosunek współczynników załamania światła ośrodka, do którego przychodzimy do ośrodka, z którego przychodzimy, więc mi wyszłoby sinalfagr=npł/npow=1,45/1.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
O tym chyba dyskutowaliśmy już w innym temacie na forum - nie ma sensu przecież rozpatrywać kąta granicznego przy przejściu z ośrodka o mniejszym n do ośrodka o większym n, bo wtedy nigdy nie dojdzie do zjawiska całkowitego wewnętrznego odbicia. Więc tu oczywiście nie będzie żadnego kąta granicznego przy przejściu powietrze-szkło, pojawi się tylko kąt graniczny (który może faktycznie nieco niefortunnie został nazwany alfa_gr, ale jednak) w przypadku padania wiązki światła na ściankę S2, czyli przy przejściu szkło-powietrze.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A mógłby Pan narysować te kąty beta, 90-beta itp. bo jakoś nie umiem tego u siebie zaznaczyć?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Czyli właściwie z tymi oznaczeniami powinno być: sin((90-beta)_gr)=1/1,45?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tak. Ale ja to wcześniej nazwałem po prostu jako alfa_gr ;)
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Spróbowałem to sparafrazować na taką odpowiedź, aby było jak najmniej pisania słownego a więcej obliczeń:

Czy w ten sposób jest ok?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Chcemy pokazać, że światło nie wyjdzie z płytki, a zatem na ścianie S2 musi dojść do całkowitego wewnętrznego odbicia. Żeby faktycznie do niego doszło, to kąt padania musi być większy od kąta granicznego. Wiemy, że sin(alfa_gr) = 1/1,45 = 0,6897, z tablic możemy zatem oszacować kąt graniczny na ok. 44 stopnie (na pewno pomiędzy 40 i 45). Chcielibyśmy zatem pokazać, że najmniejszy możliwy kąt padania jaki możemy uzyskać na ścianie S2 będzie i tak większy niż kąt graniczny. I dalej rozumowanie jest w zasadzie takie jak w rozwiązaniu - najmniejszy możliwy kąt padania na ścianie S2 uzyskamy wtedy, gdy kąt padania na ścianie S1 będzie równy niemal 90 stopni - czyli promień świetlny idący prawie równolegle do ściany S1, który jednak wpada potem do płytki. Z prawa załamania dostaniemy że sinus kąta załamania (sin(beta)) to będzie: sina(alfa)/sin(beta) = n2/n1 ---> sin(alfa)/sin(beta) = n2 (przyjmujemy, że n1 = 1, bo to powietrze). A zatem sin(beta) = sin(alfa)/n2 = sin(alfa)/1,45. Będzie to na pewno nieco mniej niż 1/1,45, bo sin(alfa) musi być nieco mniejszy od 1, bo alfa musi być przynajmniej minimalnie mniejszy niż 90 stopni. A zatem kąt beta jest na pewno mniejszy niż 45 stopni (z rozważań początkowych gdzie odczytywaliśmy dane z tabelki). Następnie kąt padania na ścianę S2 to będzie (90-beta) - wynika to z trójkąta prostokątnego. A zatem kąt padania na ścianę S2 będzie na pewno większy niż 45 stopni. Na samym początku zauważyliśmy, że kąt graniczny jest na pewno mniejszy niż 45 stopni, więc kąt padania na ścianę S2 będzie na pewno większy niż kąt graniczny, zatem dojdzie na pewno do całkowitego wewnętrznego odbicia -> światło nie opuści więc płytki.