Pytanie wielomianowe
Mam wielomian: 3(x^4+x^3+x^2+x) +4
Jak udowodnić, że jest on dodatni w x należącym do R?
Miejsca zerowe Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Wielomian ten pojawił się w takim jednym zadaniu optymalizacyjnym i właśnie miałem z nim problem.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Wskażesz w którym zadaniu? Jeszcze pokombinuje później bo znając życie da się to jakoś ładnie przekształcić wzorami skróconego mnożenia.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
I w którym miejscu tego zadania pojawia ci się powyższy wielomian? Przecież ładnie się zeruje pochodna dla x=1 i prawdopodobnie punkt P będzie miał współrzędne P(1,3)
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tez wiedziałem, że zeruje się dla jedynki tylko nie wiedziałem jak udowodnić, że tej reszty nie da się już rozłożyć. Gdy robiłem to Hornerem to taki wielomian mi wyszedł po wstawieniu jedynki.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Hmm, rzeczywiście, podejrzane troszkę to zadanie bo faktycznie wychodziłoby na to, że trzeba przeprowadzić jeszcze dowód, że jest to jedyny pierwiastek rzeczywisty.
Jak coś uda mi się wymyślić to jeszcze napiszę :/
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
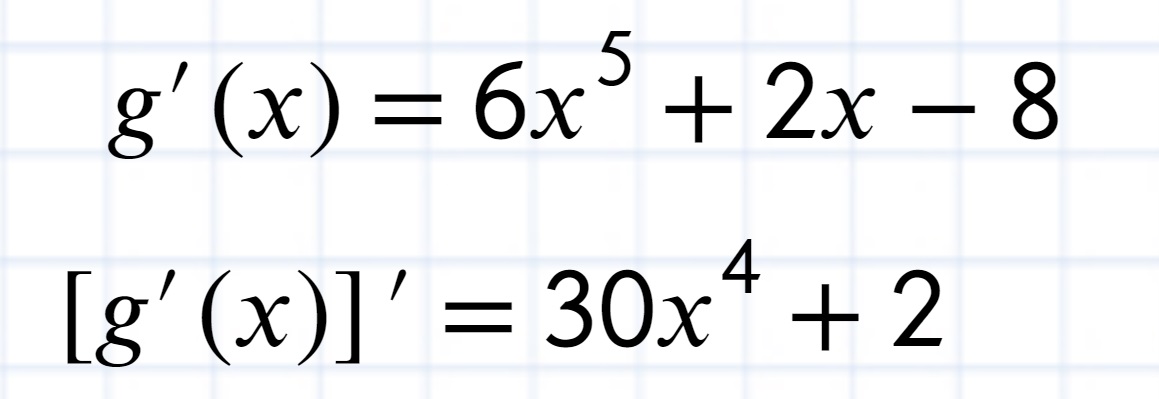
Spójrz! Pochodna pochodnej jest rosnąca w całej dziedzinie, zatem pochodna funkcji g(x) jeżeli ma miejsce zerowe =1 to jest to jej jedyne miejsce zerowe.
Nie prawda?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Prawda, nie pomyślałem o drugiej pochodnej. Dziękuję bardzo za pomoc i rozjaśnienie.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
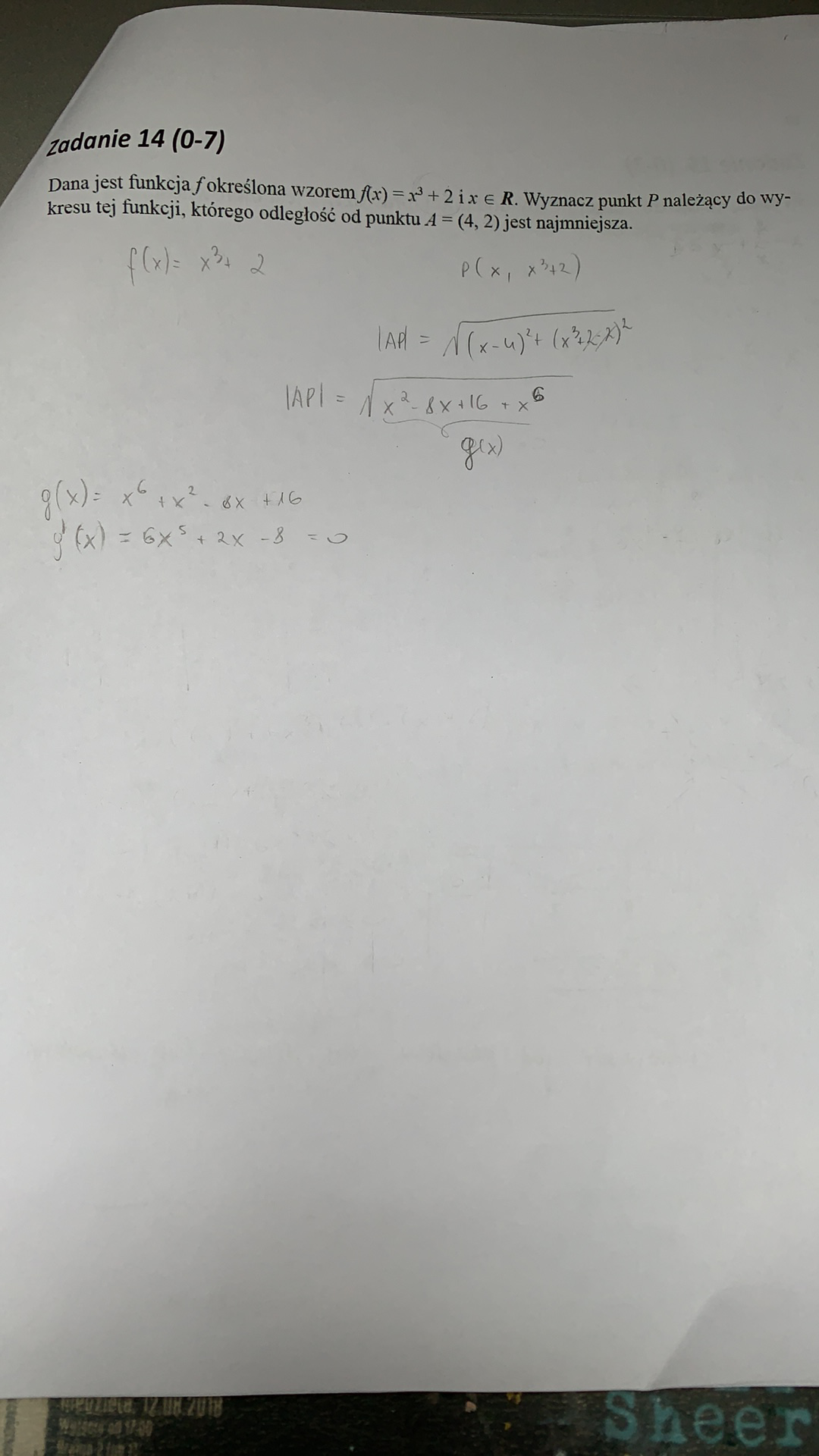
Ten dowód wymaga jeszcze weryfikacji, z ciekawości sam wymyśliłeś ten wielomian?