zad.12 arkusz 13
Dane jest równanie x3+(m-2)x2+(2m+1)x-3m=0 z niewiadomą x . Wyznacz wszystkie wartości parametru m dla których istnieją 3 różne rozwiązania tego równania spełniające warunek x1 do potegi trzeciej+x2 do potegi trzeciej+ x3 do potegi trzeciej = 82
Jak rozpisać podany warunek wzorami vieta?
matematyka Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych

W razie problemów z rozwiązaniem warunków służę pomocą :)
- 2
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
jak uzyskałeś nawias kwadratowy? rozumiem ze wyciągamy x-1 ale nie moge przejść przez to dlaczego zostaja takie liczby w nawiasie
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
W poleceniu mamy wymóg: -trzy różne rozwiązania
Jeżeli wiemy o tym, że istnieje już jedno rozwiązanie którym jest x=1 to z nawiasu chcemy uzyskać dwa rozwiązania.
Natomiast warunek delta>0 nie jest wystarczający.
Gwarantuje on nam to, że z nawiasu uzyskamy dwa różne rozwiązania ale różne między sobą . Dlatego musimy zabezpieczyć się przed sytuacją taką, gdy z nawiasu uzyskamy przykładowo rozwiązanie x=3 oraz x=1 ponieważ wtedy mielibyśmy tylko 2 różne rozwiązania.
Dlatego jeżeli zapiszemy warunek że f(1)/=/0 to wtedy mamy pewność, że x=1 nie wyzeruje nam tej funkcji czyli mamy pewność, że jednym z dwóch rozwiązań na pewno nie będzie x=1.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
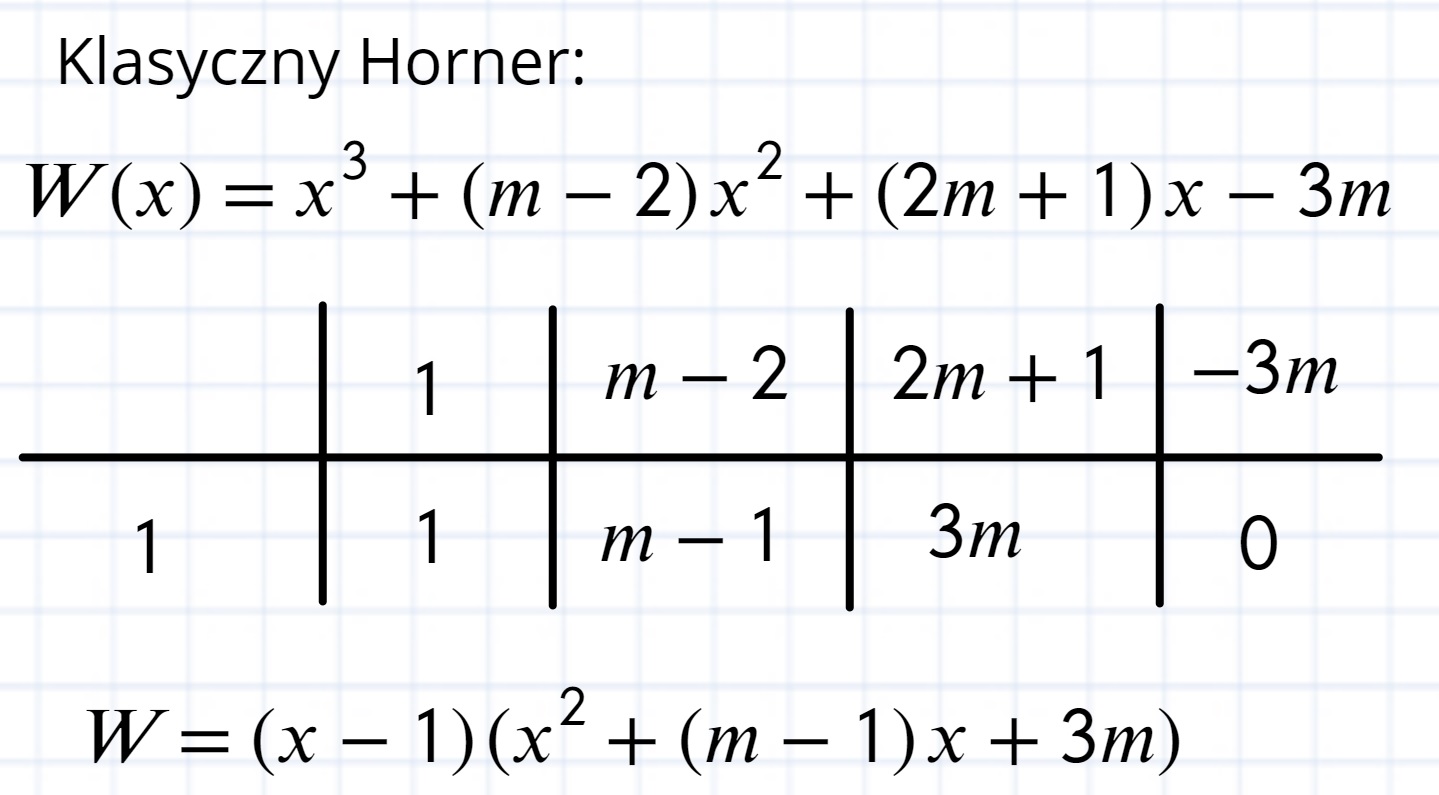
Spójrz do kryteriów jedno rozwiązanie już masz jest ono równe 1.
Zatem jeżeli warunek x1^3+x2^3+x^3=82 przekształcisz do postaci x2^3+x3^3=81 to wzory Viete'a uzyskujesz korzystając ze wzoru na sumę sześcianów :)
Jeżeli po tych wskazówkach dalej będziesz miał problem daj znać rozpiszę wszystko :)