Zadanie 10 arkusz XV
Dla jakich wartości parametru ,,m'' nierówność (2x-m)(x-3m-4)<0 jest spełniona przez każdą liczbę rzezczywistą należącą do przedziału (1;5)
Czy również komuś nie zgadza się odpowiedź z rozwiązaniem w kryteriach? I mógłby potwierdzić mi, że to literówka?
Takie mi wyszły warunki:

Jeżeli komuś również, proszę o potwierdzenie :)
zadanie z parametrem błąd w kryteriach Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Mógłbyś rozpisać całe zadania i wytłumaczyć skąd się co bierze?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
1) czy warunek z delta jest potrzebny? warunek z f(1) i f(5) gwarantuje juz nam chyba dwa miejsca zerowe?
2) nie rozumiesz czemu w tych warunkach nie mamy nierówności ostrej
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
1) W tym konkretnym zadaniu nie jest potrzebny
2) nie ponieważ nierówność nieostra spełnia to zadanie (np. m=2 spełnia zadanie)
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Wytłumaczy ktoś dlaczego używamy założeń z f(1) i f(5)? Nie mogę w ogóle tego zrozumieć.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
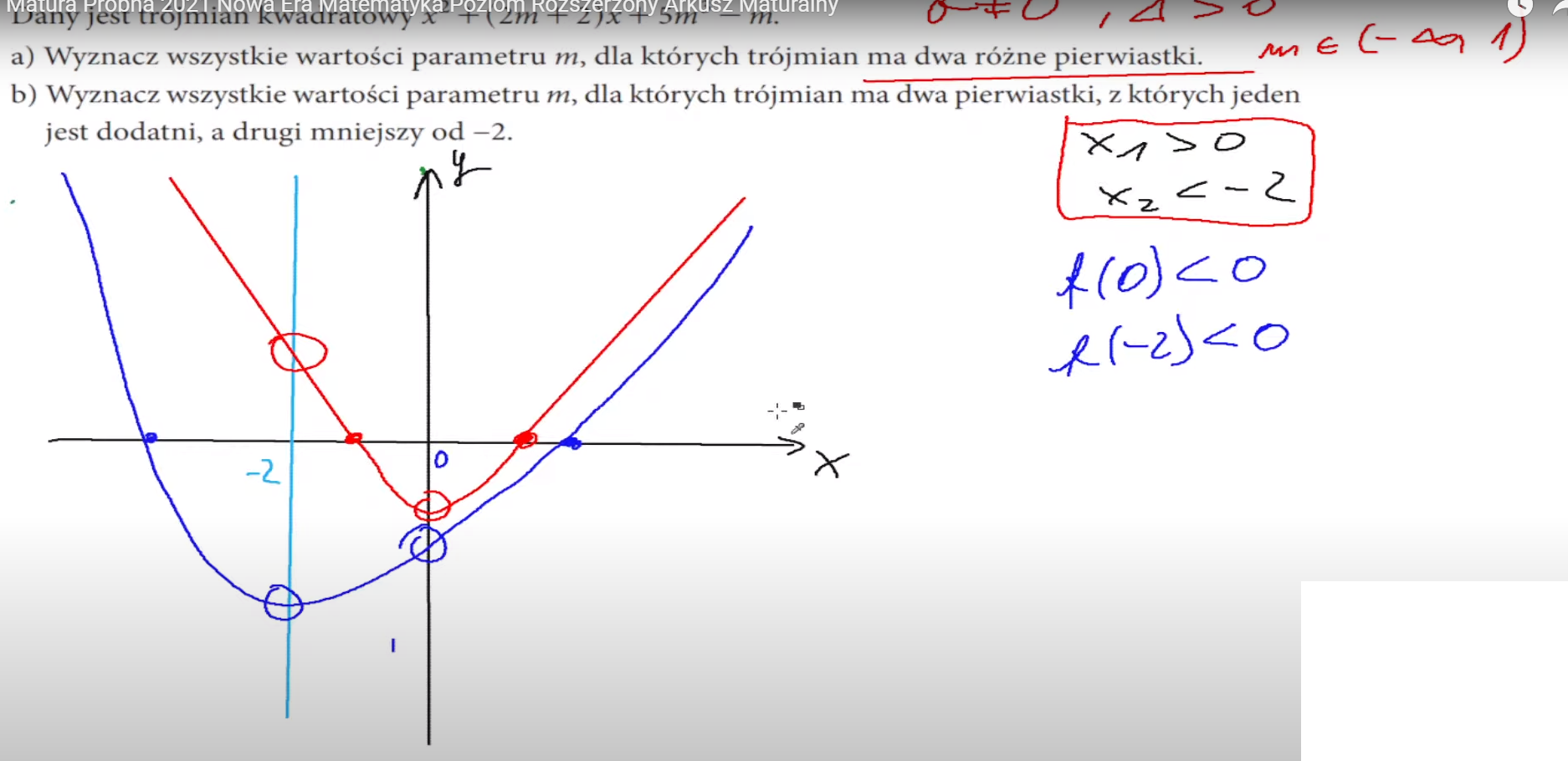
@aaadm Zobacz proszę na mój powyższy rysunek poglądowy. Tak wygląda każda funkcja spełniająca treść zadania. To stąd wynikają te warunki. Pisz jeśli masz dalsze pytania :)
- 2
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
czym te zadania się różnicą ze w naszym zadaniu mamy nierownosc nieostra a w tym ostra?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
@jarosinski nadal nie rozumiem, skoro przedział jest obustronnie otwarty (1;5) i do tego w równaniu mamy nierówność ostrą to dlaczego zapisujemy nierówność nieostrą w f(1)<=0 i f(5)<=0?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
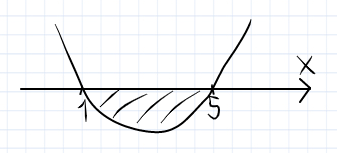
Rozpatrzmy skrajny przypadek, gdy f(1) = f(5) =0. Wtedy jest spełniona przez każdą liczbę rzeczywistą należącą do przedziału (1;5) zatem zachodzi treść zadania.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
@Grzegorz.p7 w tym zadaniu z NE, które wysłałeś to miejsce zerowe maja spełniać jakieś konkretne warunki, a w zadaniu z ksiażki to wartości funkcji maja należeć do przedziału (1,5). Zauważ że gdy F(1)=0 i f(5)=0 to nadal mamy przedział (1,5). Z kolei w twoim zadaniu jeśli x1>0 to f(0) nie może być równe 0 - musi być mniejsze

- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
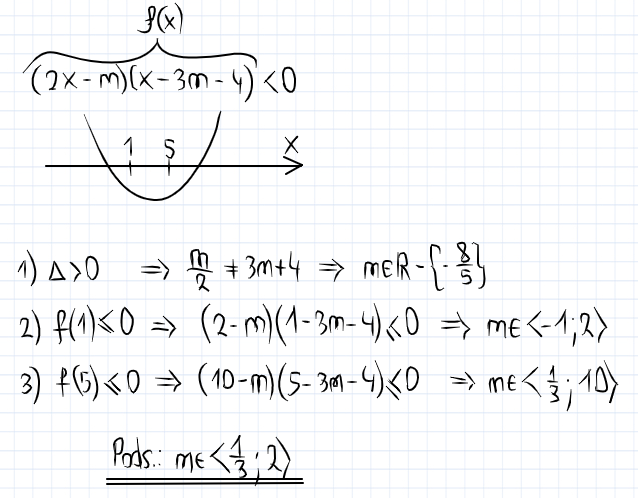
Masz rację, ostateczna odp powinna być < 1/3 ; 2>