dsegvef 480 wyśw.
09-04-2021 17:31
Aksjomat VI zad. 9
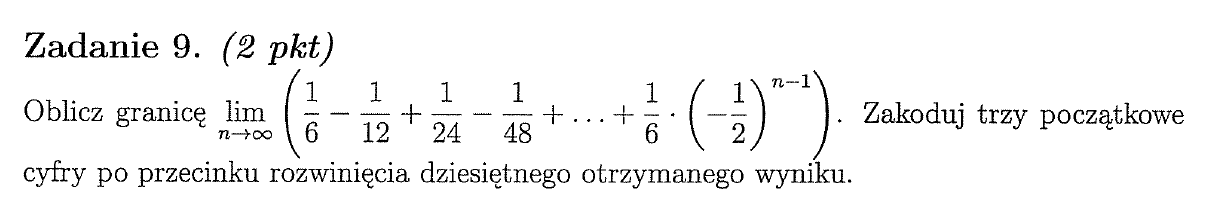
Czy ktoś mógłby mi wytłumaczyć, jak zrobić to zadanie? Odpowiedź to 111
matematyka Dodaj post do ulubionych Poproś o pomoc
Kliknij tutaj, aby dodać nowy komentarz.
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
epsilon
09-04-2021 22:39
Goshh
22-04-2022 21:01
Dlaczego to jest szereg? W sensie nie rozumiem dlaczego ponieważ zawsze on też inaczej wygląda na koncu (+...).
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
N∆T∆LI∆
24-04-2022 19:39
Podbijam, jak zorientować się że jest to szereg?
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
epsilon
25-04-2022 10:19
Szereg geometryczny ma postać: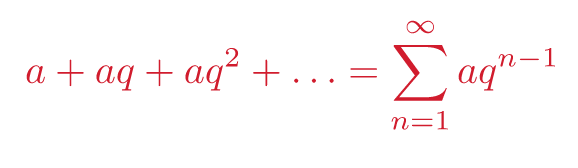
. Trzeba więc zauważyć, że każdy kolejny składnik sumy to poprzedni składnik pomnożony przez stały iloraz q = -1/2, którego moduł jest mniejszy od 1.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
jarosinski
25-04-2022 11:07
Szereg jest sumą wszystkich wyrazów ciągu geometrycznego. Jest zatem sumą nieskończenie wielu wyrazów ciągu. Zatem jest granicą (gdzie n-> niesk) z Sn, gdzie Sn- suma n-tych wyrazów ciągu geom. Dlatego zawsze gdy jest granica z sumy ciągu geom to chodzi o szereg (dokładnie w taki sposób wyprowadzałem wzór na szereg na zajęciach).
- 2
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych