Arkusz XVIII zadanie 14
W pociągu są 2 ponumerowane wagony w każdym wagonie są 2 ławki po 3 miejsca. Ile jest możliwości ułożenia 8 pasażerów tak aby tylko jedna ławka była zajęta w całości.
Czy mógłby ktoś powiedzieć co jest nie tak w poniższym rozwiązaniu?
Ciężko mi połapać się z rozwiązania w kryteriach co uznajemy za rozróżnialne a co nie.
1) Czy dwie ławki w wagonie uznajemy za różne czy nie?
2)Czy miejsca na ławkach uznajemy za rozróżnialne czy nie?
Rozwiązałem to zadanie w ten sposób:
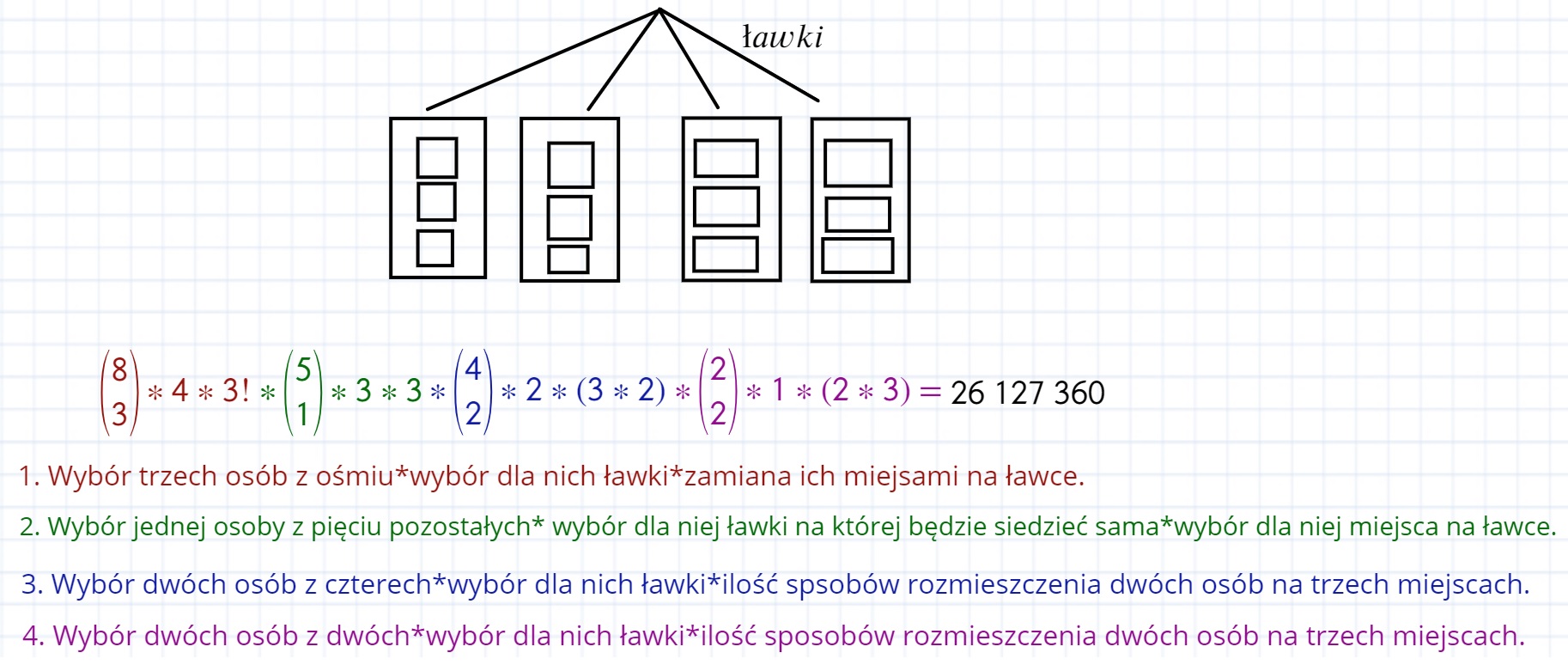
I z mojej obserwacji wynika, że w kryteriach dla części osób potraktowano miejsca na fotelach jako rozróżnialne a dla części już nie.
EDIT: W rozwiązaniu na obrazku niepotrzebnie pomnożyłem w niebieskiej części przez 2. Ponieważ, nie ma znaczenia którą ławkę wybierze wybrana dwójka, gdyż zawsze pozostali pójdą na ostatnią, zatem moim zdaniem ostatecznym wynikiem powinien być wynik : 13 063 680
kombinatoryka niejasność Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Czyli ten wynik: 13 063 680 jest poprawny?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tutaj też jest trochę kwestia interpretacji wyboru ławek, więc w zależności od niej wynik 13 063 680 lub 26 127 360 będzie prawidłowy
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A z czego wynika ta różnica?
Wynik 13 063 680 to wynik dla rozróżnialnych ławek, miejsc.
Przy jakiej koncepcji wynik 26 127 360 jest poprawny?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Przemyślałem i wynik 13 063 680 jest prawidłowy :)
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A ja mam pytanie, dlaczego w tej niebieskiej części jednak nie mnożysz razy 2?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Spójrz:

Jeszcze dla jasności:
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Można jeszcze w ten sposób:
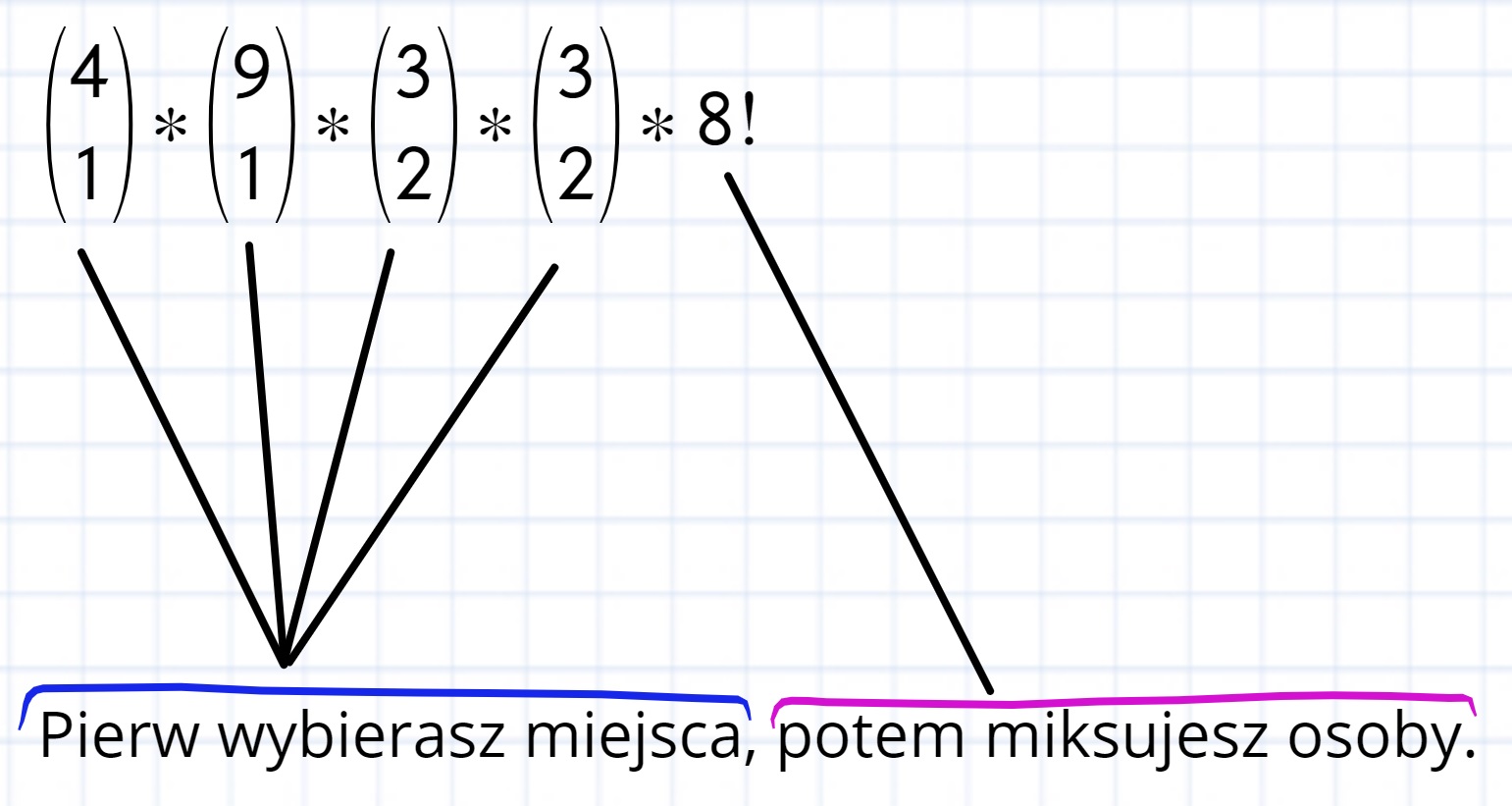
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Czyli przyjmujemy, że powiedzmy na pierwszej ławce ląduje A,C, na drugiej B,D, to takie samo zdarzenie jak C,A i D,B? A skoro to takie samo zdarzenie, to dlaczego w ławce, gdzie są 3 osoby mnożymy razy 3! ?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
,,Czyli przyjmujemy, że powiedzmy na pierwszej ławce ląduje A,C, na drugiej B,D, to takie samo zdarzenie jak C,A i D,B?''
-Tak, zamianą osób na miejscach zajmujemy się dalej. Pierw rozdzielamy je pomiędzy ławkami a dopiero w dalszym kroku zamieniamy je między sobą.
A skoro to takie samo zdarzenie, to dlaczego w ławce, gdzie są 3 osoby mnożymy razy 3! ?
Nie wiem czy dobrze Cię rozumiem. Mnożymy razy 3! ponieważ zamieniamy osoby między sobą na ławce.
Spójrz w każdym kroku pierw wybieram na ile sposobów mogę wybrać trójkę lub dwójkę osób.
W naszym przypadku jeżeli korzystamy z kombinacji to nie ma znaczenia czy wybierzemy BCA czy CAB bo to kombinacja, dopiero w kolejnym etapie naszego "wymnażania" uwzględniamy kolejność i po wybraniu przykładowo BCA na jedną ławkę zamieniamy wybrane osoby między sobą na 3! sposobów.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Chyba za głupi jestem, żeby pojąć to, chociaż bardzo spodobał mi się sposób, najpierw miejsca potem same osoby na 8!. Dziękuję bardzo i tak :D Może to zadanie zostanie wybrane jako to, które omówimy na lekcji i wtedy mi się ostatecznie rozjaśni.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Czy można to zadanie zrobić tak że najpierw obsadzamy jedną z 4 ławek np. 1, miksujemy te 3 osoby a potem każda z pozostałych 5 osób ma do wyboru miejsca na pozostałych ławkach (pozostało 9 miejsc) czyli 1 ma 9 sposobów druga 8 sposobów itp. A na końcu odjąć sytuacje gdzie te osoby zajmują całą ławkę (czyli przypadki gdzie zajeli 2 3 lub 4 ławkę)?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Zerknąłbyś @... czy moje rozumowanie jest logiczne ? I czy rozumowanie poprawne, niby wynik ok ale różnie bywa ;)
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Rozumowanie masz OK, w kryteriach rzeczywiście jest problem z rozróżnialnością miejsc na ławkach