Arkusz XIII zadanie 14
Punkty A (-4; 1), B (4; 7) są wierzchołkami trójkąta równoramiennego ABC, w którym |AC|=|BC|. Pole tego trójkąta jest równe 60. Oblicz współrzędne środka okręgu opisanego na trojkącie ABC. Rozważ wszystkie możliwe przypadki.
 Hej, mam trochę braki w geometrii analitycznej, możliwe że nie rozumiem czegoś prostego. W tym zadaniu doszłam do wyznaczenia równania symetralnej odcinka AB, ale skąd wziąć równanie okręgu, które jest podane w kryteriach? Dlaczego akurat ten okrąg ma środek w punkcie (-4; 1)?
Hej, mam trochę braki w geometrii analitycznej, możliwe że nie rozumiem czegoś prostego. W tym zadaniu doszłam do wyznaczenia równania symetralnej odcinka AB, ale skąd wziąć równanie okręgu, które jest podane w kryteriach? Dlaczego akurat ten okrąg ma środek w punkcie (-4; 1)?
Matematyka geometria analityczna matura Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Jeżeli chodzi o rozwiązanie z kryteriów to zrobiono to w ten sposób: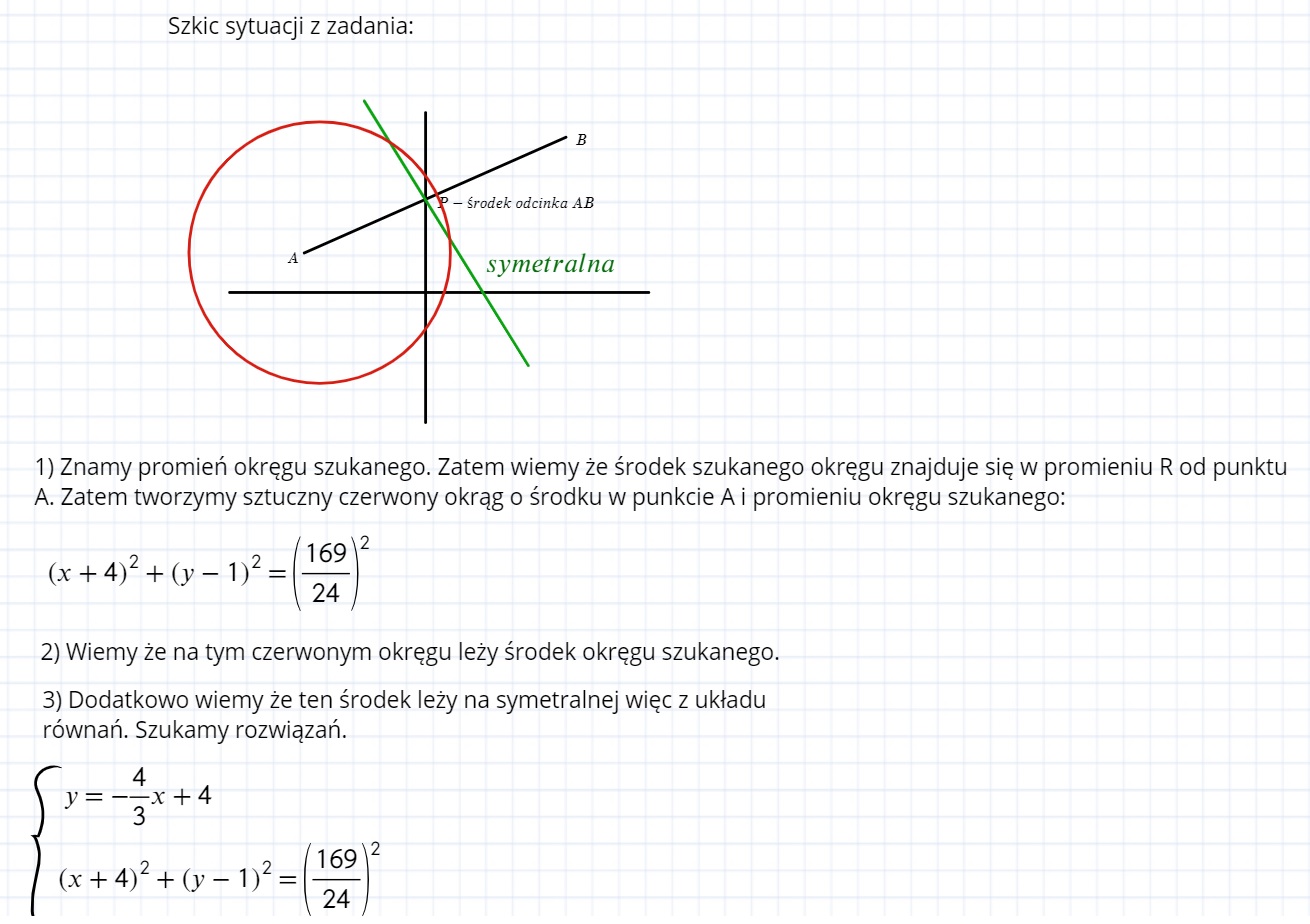
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Teraz już wszystko rozumiem, dziękuję Ci bardzo za poświęcenie czasu na szczegółowe wyjaśnienie :)
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Rzeczywiście kryteria mogą trochę wprowadzać w błąd.
To nie okrąg ma środek w punkcie (-4,1) bo środka tego okręgu dopiero szukasz.
Spójrz jakie masz informacje:
Wiesz że trójkąt jest równoramienny, masz współrzędne punktu A i B oraz symetralną.
Wiesz, że trzeci wierzchołek leży na symetralnej! (Ponieważ w trójkącie równoramiennym symetralna podstawy jest jego wysokością.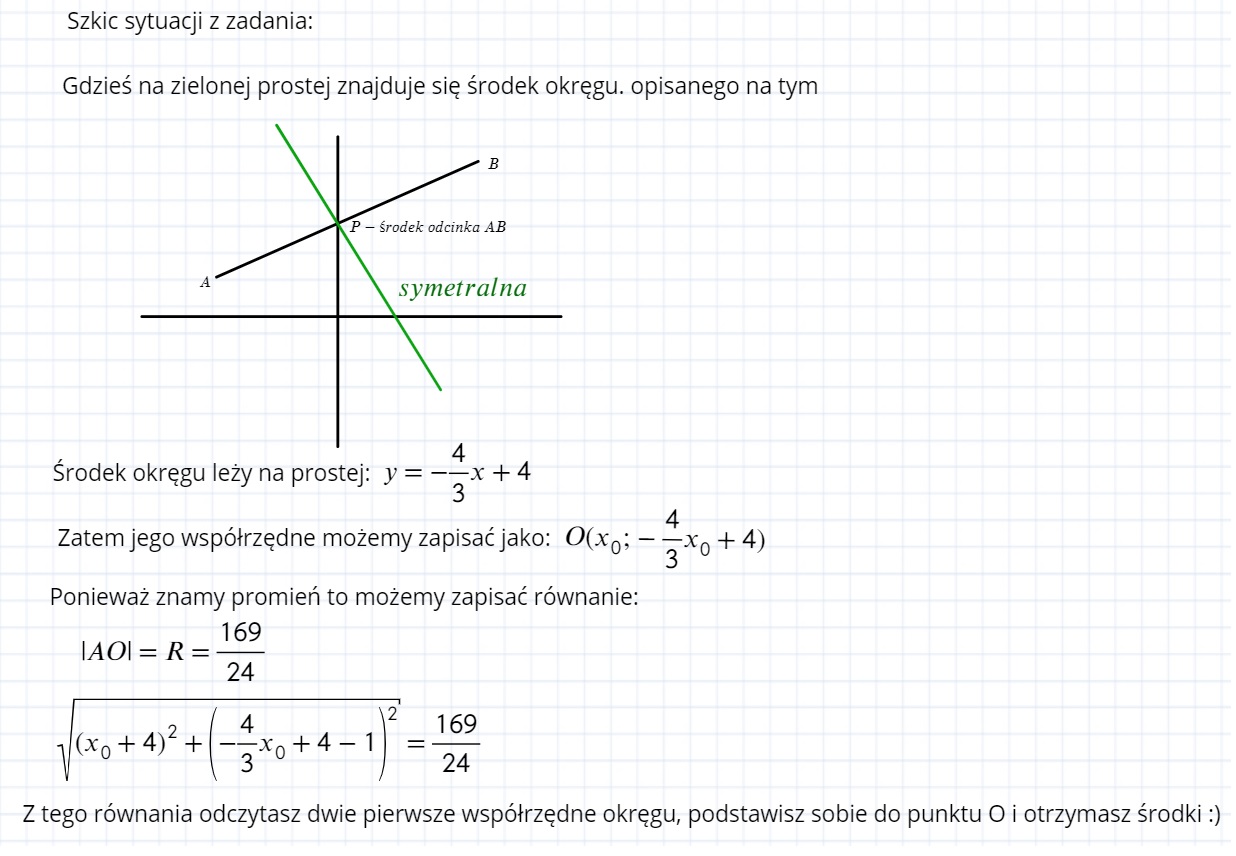
Zatem wiesz że środek okręgu leży na symetralnej oraz wiesz że odległość każdego wierzchołka od środka okręgu jest stała równa promieniowi to możesz zapisać taki układ równań: