Arkusz2015 ckepróna z4

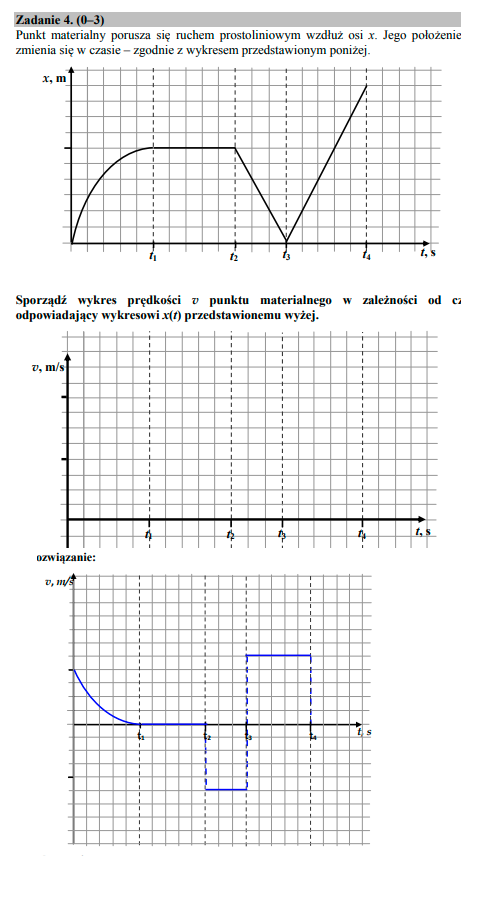
Nalezy tutaj zauważyć, że mamy przedstawiony wykres x(t), czyli położenia ciała wzdłuż osi x-ów. Tak więc na wykresie widzimy, że ciało jedzie z jakąś prędkością t0, ale w t1 już zwolnił do zera, bo x jest stały - stąd wnioskujemy że był to ruch opóźniony. (wiemy, że Δx nie zmienia się jednostajnie, dlatego ΔV tak samo ->wykres jest hiperbolą).
Kolejne fragmenty są chyba już jasne?
w t1->t2 Δx = 0 -> v=0
w t2->t3 Δx<0 => v<0
w t3->t4 Δx>0 => v>0 i takie samo jak w wyżej, bo dla połowy czasu pokonało taką samą drogę