zad 12, arkusz XVI
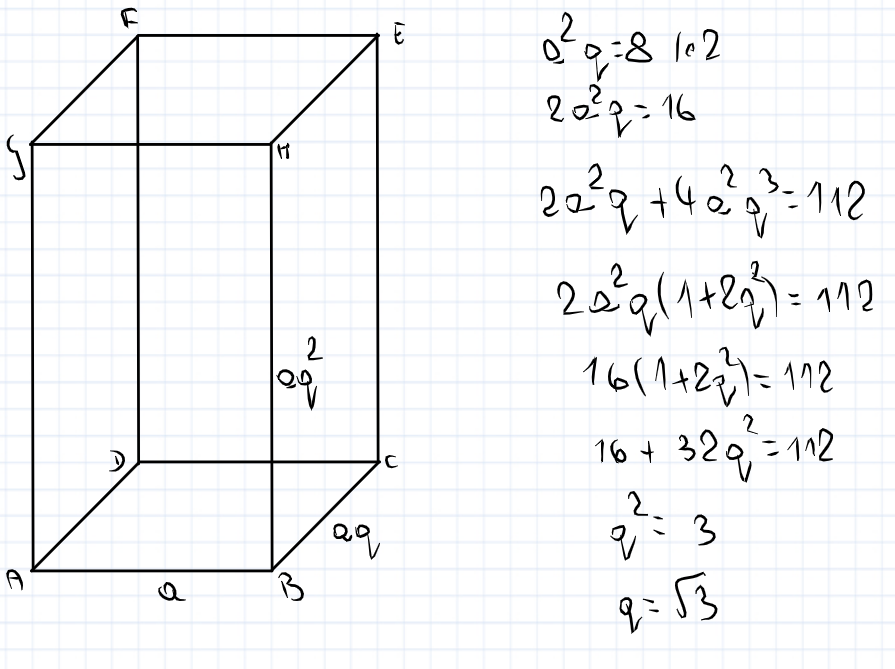
Mógłby wkazać mi ktoś błąd w odpowiedzi wychodzi q = 2, a mi uparcie q = sqrt(3)
matematyka Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
aaaa rzeczywiście, ale sie wyłożyłem na głupocie, dzięki wielkie
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
co jeśli oznaczymy boki inaczej np: BH będzie równe aq?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
nie ma to zadnego znaczenia jakie oznaczenia przyjmiesz, wazne zebys dobrze oznaczyl i wyjasnil
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Właśnie jak oznaczymy podstawę jako: a x aq^2, a wysokość jako: aq to wychodzi inna objętość. Pytanie gdzie w takim rozumowaniu jest błąd.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Zgadza się, jeśli przyjmiemy inne oznaczenia to odpowiedź będzie inna od tej przedstawionej w odpowiedziach
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
czy to zadanie można zrobić tak że gdy podstawę oznaczymy a i aq^2 a wysokość aq to pole podstawy jest 8=(aq)^2 a objętość to będzie V= a *aq *aq^2 więc też V= (aq)^2 * aq więc V=8* aq a aq jest pierwiastkiem z 8 więc V=8*2 pierwiastki z 2?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
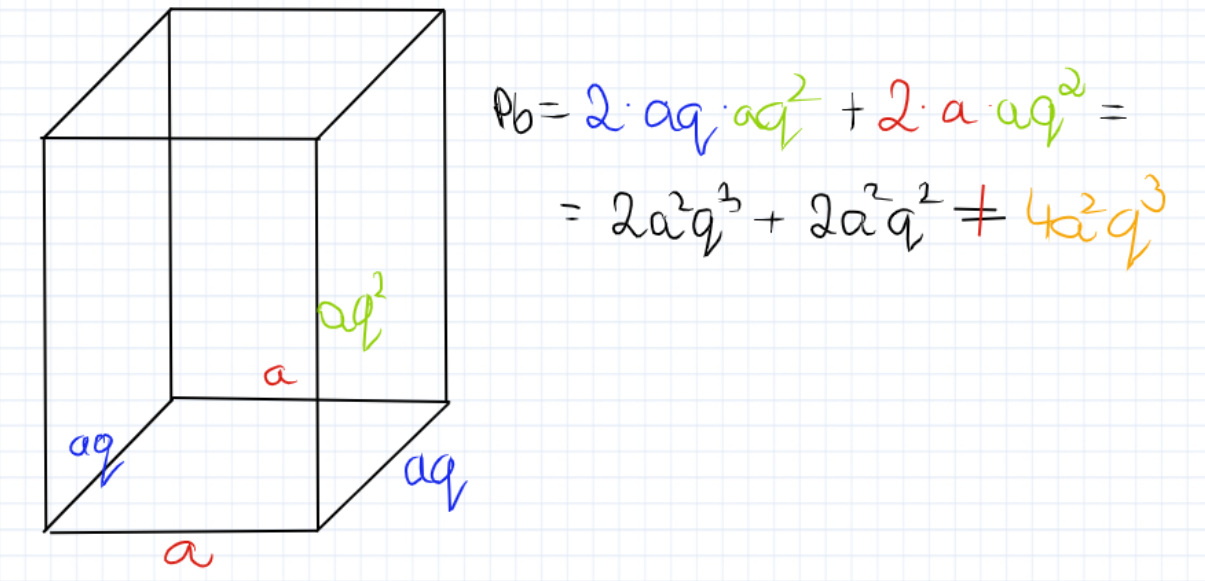
masz na bokach dwie sciany aq i aq^2 i dwie sciany a i aq^2 (podstawa prostokąt)