ZioloPan 584 wyśw. 15-04-2021 19:14

Zad 12 Arkusz II


Czy da się to zadanie zrobić innym sposobem ? Np. z pochodnej? Tyle zrobiłem i nie wiem czy da się to dalej ruszyć bo skoro nie ma ekstremum to nie wiem jak wyliczyć Zwf.


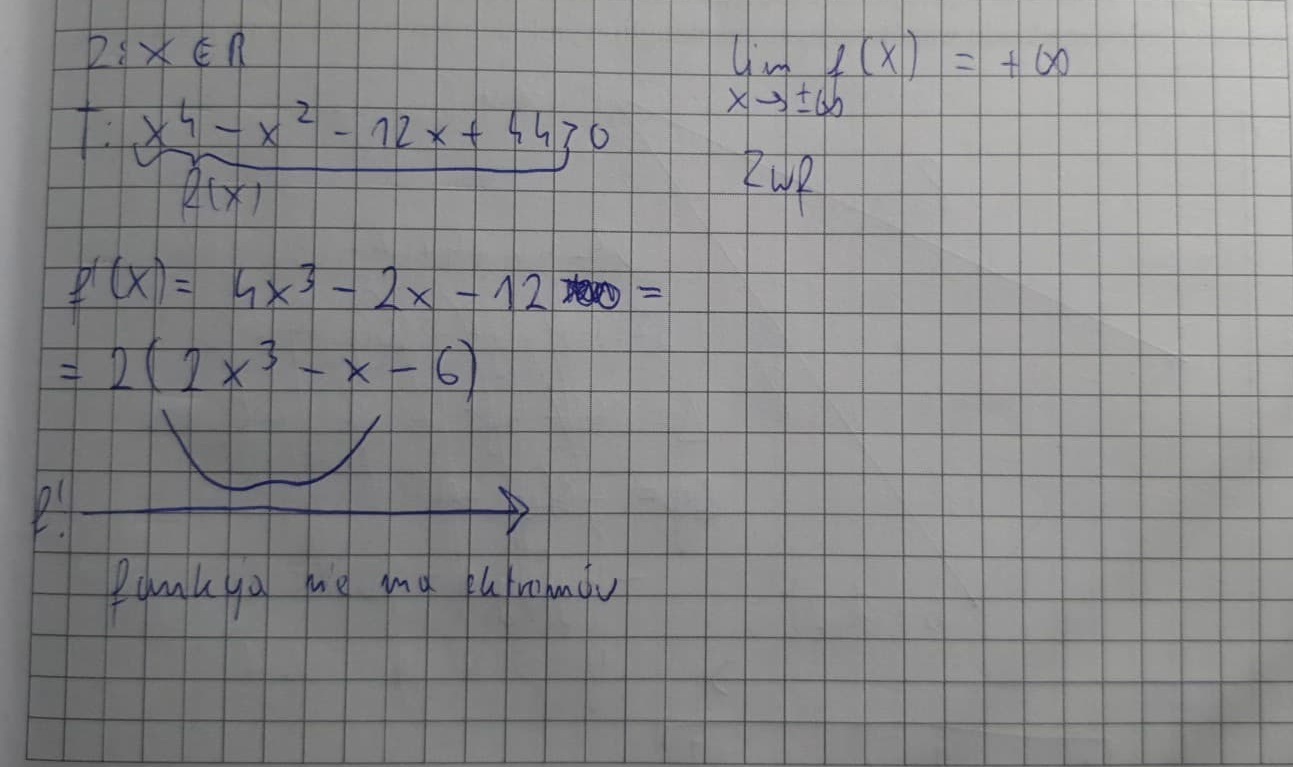
Matematyka Dowody Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
ZioloPan 15-04-2021 23:01

Wolfram wypluwa coś takiego, zatem funkcja ma minimum lokalne tym punkcie, wpisując w kalkulator i licząc f(1,5576) oraz limf(x) zwf wychodzi rzeczywiście <~30 ; +niesk.)  

Zatem moje 2 pytania: 

- Czy jest jakieś matematyczne narzędzie które pozwoliło by nam obliczyć pierwiastek tego wielomianu w tym przypadku?

- Czy jest może inny sposób na to zadanie oprócz grupowania wyrazów? 

jarosinski 24-04-2021 22:49

Witam, jeśli chcemy już skorzystać z metody rachunku różniczkowego do dowodzenia tego zadania to jedyną opcją (mając nasze umiejętności) byłoby oszacowanie miejsca zerowego pochodnej oraz wartości funkcji dla tego argumentu i w ten sposób udowodnienie, że jest zawsze >0.


I odpowiadam jeszcze na dwa pytania:

- jest algorytm, ale jest dla was niedostępny (opiera się o liczby zespolone). Wy możecie co najwyżej przybliżać miejsce zerowe

- nie