Zad 8 Arkusz XXII

Czy to Ci wystarcza?

@<3 

nie powinniśmy w założyć że t jest różne od 0?

@kuba1337

a dlaczego chcesz zrobić takie założenie?

bo cos(x) jest w mianowniku

W mianowniku jest funkcja kwadratowa z cos czyli, aby ten ułamek musiał istnieć to jego pierwiastki muszą być różne od zera czyli t1 i t2 nie należą do dziedziny. Ja to rozumiem w ten sposób 

Dlaczego należy policzyć lim x->1?

Ponieważ coś/"0"=nieskończoność ze znakiem odpowiednim. Mnie bardziej zastanawia czemu tu ktoś liczył lim x->1 a nie po prostu g(1).

Dlaczego liczymy limx->1? Czy ma to związek z tym, że t należy do zbioru [-1,1], więc chcemy znaleźć ,,górną” wartość naszego zbioru wartości w określonej dziedzinie? I stąd liczymy granicę dla argumentu 1?

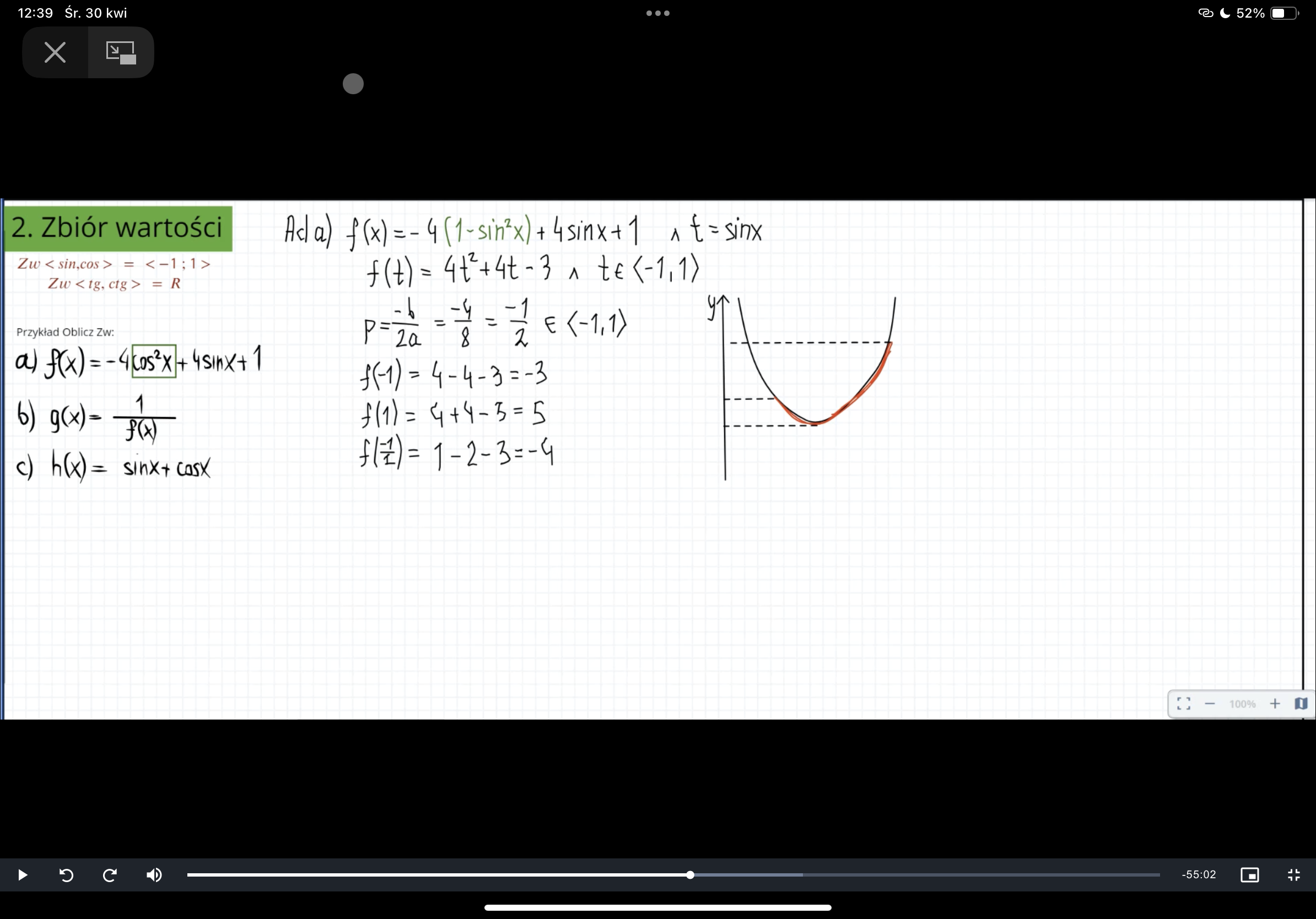
@Artur Chyba już rozumiem. Można zrobić to tak, jak na screenie powyżej - obliczyć q oraz f(-1) i f(1). Ale w zasadzie limx->1 zadziała w tym wypadku dokładnie tak samo, jak f(1). Pytanie tylko, czy tak będzie w każdym przypadku?

Moim zdaniem to działa tak samo, ale tutaj granica nie będzie poprawna, bo granice liczymy dla przedziałów otwartych a wartości funkcji dla zamkniętych, ale to tylko moje zdanie.