Arkusz XXII zadanie 9
Uzasadnij, że funkcja określona wzorem f(x)= 4x^100 -5x^80 +2 nie posiada pierwiastków rzeczywistych
Robiac to zadanie doszedłem do takiej postaci i napisałem zdanie:
Jedynymi pierwiastkami f(x)' sa liczby x {-1,0,1}, zatem jeśli f(x) ma ekstrema to sa nimi wartości dla argumentów z tego zbioru
To wystarczy, czy może jednak muszę sprawdzać dalej to, czy fioletowe nawiasy maja jakieś pierwiastki?
wielomiany pierwiastki Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
O coś się nie załadowało i nie wkleił się screen. Generalnie schemat zrobienia tego zadania znam tylko chodzi mi o to czy muszę dalej to jakoś grupować / udowadniać że filoetowe nawiasy nie maja pierwiastków?
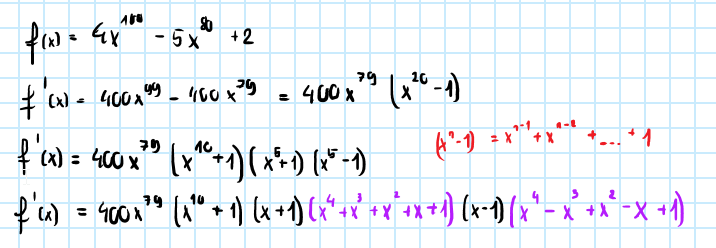
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
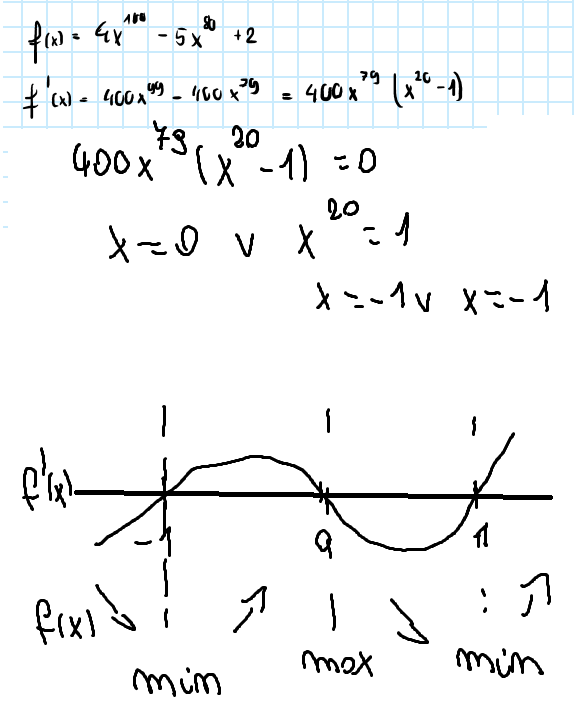
troche nie rozumiem co napisałeś ale chodzi, żebyś te argumenty sprawdził czyli minima lokalne jakie wartości przyjmują, tzn załóżmy ze w argumecie 0 jest minimum to liczysz f(0) jaka wartośc przyjmują i musisz policzyć jeszcze granice w nieskonczonościach ale skoro potega jest parzysta to w obu nieskonczonosciach jest +oo, i na koniec wypisanie zwf c.k.d