UJ 2020 zadanie 8.3 2

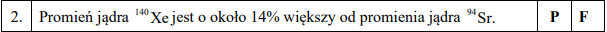
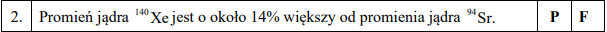
Wspominałem o tym na zajęciach - nie ma tego w podstawie programowej, więc w takiej formie nie mogłoby się to pojawić na maturze. A wyliczyć można to tak, że można założyć, że jądro to kula, którego objętość jest wprost proporcjonalna do liczby nukleonów (czyli liczby masowej A). Czyli mamy, że V ~ A. Ponieważ objętość kuli to V = 4/3 * pi * R^3, to oznacza to, że V ~ R^3, a stąd widzimy, że R^3 ~ A, a zatem R jest proporcjonalne do pierwiastka trzeciego stopnia z A. Czyli należałoby sprawdzić, czy pierwiastek 3 stopnia ze 140 jest faktycznie 1,14 razy większy od pierwiastka trzeciego stopnia z 94. W istocie tak jest, ale tu pojawia się kolejny problem eliminujący to zadanie z matury - na kalkulatorze prostym nie mamy przecież możliwości policzenia pierwiastka trzeciego stopnia.