16.67 Krysicki
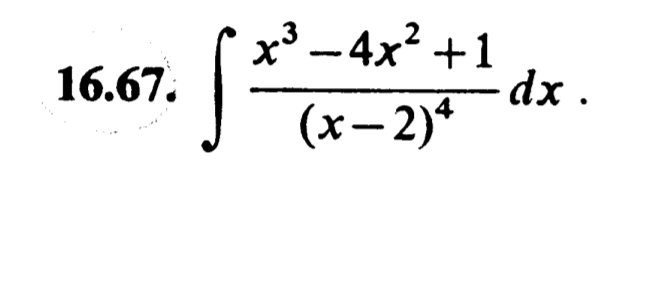
hej,
poprosiłabym o pomoc w rozwiązaniu tego przykładu
Z góry bardzo dziękuje
całki Dodaj post do ulubionych Poproś o pomoc
- 5
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Mam nietypowe pytanie czysto z ciekawości. Jak można by obliczyć miejsca zerowe wielomianu na górze czyli x^3 -4x^2 +1. Kalkulator wypluł dość dziwne liczby, a także tradycyjne metody nie za bardzo działają.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Jest metoda (analogiczna do delty tylko duuużo trudniejsza) obliczania pierwiastków równań 3 stopnia oparta o liczby zespolone. Jest nawet w Krysickim. Trzeba by z tej metody po prostu skorzystać
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
@jarosinski może Pan jakoś wytłumaczyć z czego wynika tak dziwny rozkład? Dodatkowo na lekcji mówiliśmy, że stopień licznika musi być o 1 mniejszy niż stopień mianownika. Tutaj mamy drugą, trzecią, czwartą potęgę, a w liczniku tylko stałe.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ogólnie wynika to z własności funkcji wymiernych:

- 2
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Na jakiej podstawie my stwierdzamy, że mają być cztery ułamki z takimi ułamkami? Skąd mamy to wiedzieć?
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Zawsze jak mamy n-tą potęgę w mianowniku to rozkładamy na n ułamków stopnia mniejszego bądź róznego n - można to przeanalizować, że żaden inny rozkład nie będzie dawał powodzenia
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Może to jest proste, ale nie rozumiem dlaczego stopień licznika musi być o 1 mniejszy niż stopień mianownika?
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ponieważ później robiąc wspólny mianownik i porównując liczniki nie mielibyśmy równości wielomianów. Dokładniej: współczynniki przy wyższych potęgach i tak by się wyzerowały. Czyli specyfika matematyki tego problemu nam serwuje taki efekt
- 2
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Dziękuję:)
Chciałam jeszcze dopytać co do tego specyficznego rozkładu na ułamki proste - z jakich własności funkcji wymiernych on wynika?
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Więcej o tym można poczytać tutaj:
https://epodreczniki.open.agh.edu.pl/handbook/9/module/101/reader
- 2
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Dlaczego w rozwiązaniu 16.12, które Pan wstawił najpierw określają dziedzinę x!=1 i x!=-1 a potem podstawiają w pierwszym punkcie x=1 i x=-1 aby obliczy A i D? I czy tego nie można rozłożyć tylko na ułamki z mianownikami (x-1)^3 i (x+1)? Bo jeśli tak to nie wiem jak w podobny sposób rozwiązać 16.67
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Dziękuję, jednak dalej nie do końca rozumiem, skąd wynika, że jeżeli w mianowniku jest czynnik liniowy (x-a)ᵏ o krotności k, to w rozkładzie na ułamki proste w mianownikach występują kolejne potęgi (x-a)?
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Wynika to z uwagi 1 powyższego linku. Dowód nie jest łatwy (choć wykonalny). Możesz go wykonać lub przyjąć to twierdzenie za pewnik :)
- 2
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Wydaje mi się, że ten link nie do końca odpowiada na moje pytanie do różnych postów np 16.93 gdzie nie wiem dlaczego nie można x⁴+64 rozłożyć na iloczyn wielomianu 3 stopnia i funkcji liniowej tylko koniecznie musi być to iloczyn dwóch funkcji kwadratowych?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Proszę Pana, prosiłabym o wskazówkę jak wykonać taki dowód, w którym kierunku pójść, bo chciałabym ten dowód przeprowadzić
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
@Artur: odpowiedziałem Ci pod tamtym postem, to zupełnie inne zapytanie :)
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
@Maria: Jak podaje Google:
Dowód twierdzenia o rozkładzie funkcji wymiernej na ułamki proste jest złożony i opiera się na algorytmie dekompozycji, który polega na rozkładzie mianownika na czynniki (liniowe i kwadratowe nierozkładalne), a następnie wyrażeniu funkcji wymiernej jako sumy ułamków prostych odpowiadających tym czynnikom.
- 2
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tutaj jest specyficzny rokład na ułamki proste: