ZZ26 str 28, Kurs maturalny

---

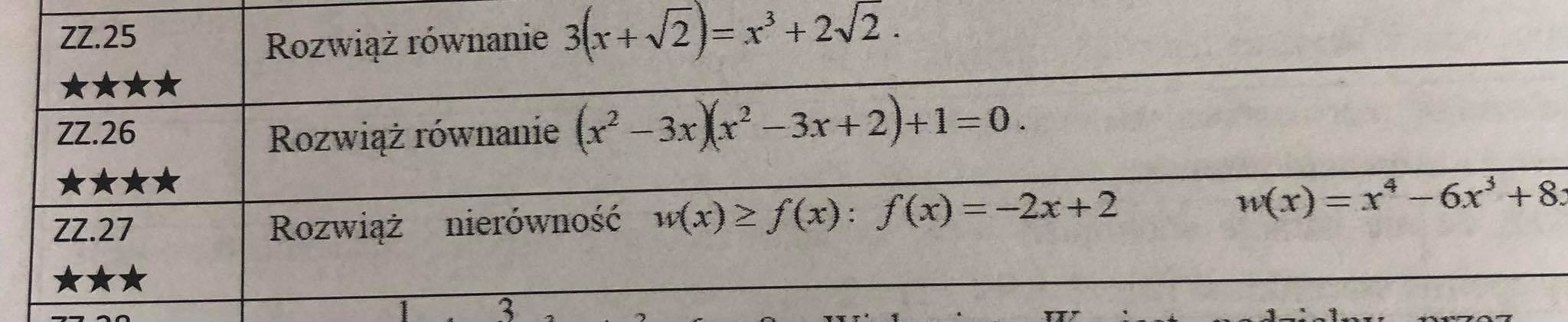
Zastanawiam się nad poprawnością mojego rozwiązania. W równaniu (x^2 - 3x)*(x^2 - 3x + 2) + 1 = 0 rozbiłam sobie nawiasy na postaci iloczynowe, co dało (x-3)(x-2)(x-1)x = - 1, czyli liczby w nawiasach to cztery kolejne liczby, które różnią się od siebie o 1. Takie liczby, gdyby były ułamkami nie mogłyby dawać -1, więc muszą być to liczby całkowite. Jedynymi liczbami całkowitymi, których iloczyn daje -1 są 1 i -1, zatem x^2 - 3x = 1 i x^2 - 3x +2 = -1 lub na odwrót: x^2 - 3x = -1 i x^2 -3x +2 = 1. W przypadku jednego zestawu równań wychodzi zbiór pusty, w przypadku drugiego wychodzi x^2 - 3x + 1 dla obu równań co daje nam x = (3-pierw z 5)/2 lub x = (3 + pierw z 5)/2 co jest poprawnym wynikiem. Czy to rozwiązanie jest poprawne merytorycznie?

---

wielomiany matura zbiór zadań cke Dodaj post do ulubionych Poproś o pomoc