regor 520 wyśw. 16-10-2021 19:30

21/2020S.1.4


Proszę o wskazanie prawidłowej odpowiedzi, ponieważ w podręczniku nie znalazłem informacji odnoście starej matury i pokazanie dlaczego dane rozwiązanie jest prawidłowe. Pozdrawiam 

Wykres Ek Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
s.gugula 17-10-2021 14:32

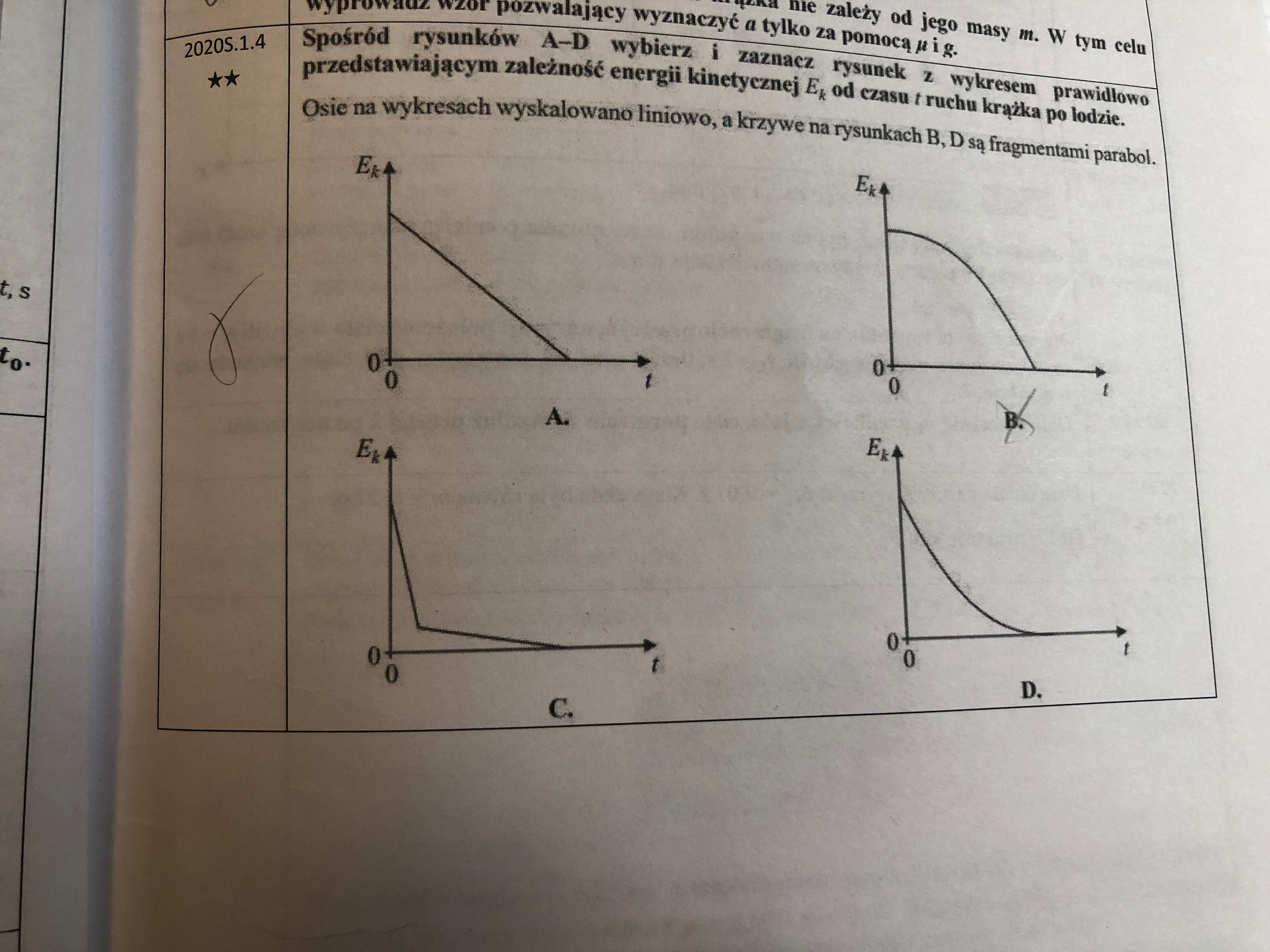
Faktycznie wygląda na to, że nie ma w książce odpowiedzi do tego zadania... w każdym razie odpowiedzią poprawną jest odpowiedź D. Można to wywnioskować stąd, że Ek = mv^2/2, a wiemy jaką zależnością od czasu opisywana jest prędkość w ruchu jednostajnie opóźnionym: v = v0 - at. A zatem jeśli podniesiemy tę prędkość do kwadratu, to dostaniemy v^2 = v0^2 - 2*v0*at + a^2*t^2 - jak widać jest to funkcja kwadratowa czasu, gdzie ramiona paraboli są skierowane w górę (przy t^2 stoi współczynnik a^2, który jest dodatni). Taką parabolę widzimy właśnie na wykresie D.