Michał_S 616 wyśw. 30-10-2021 15:12

1 c) str. 83


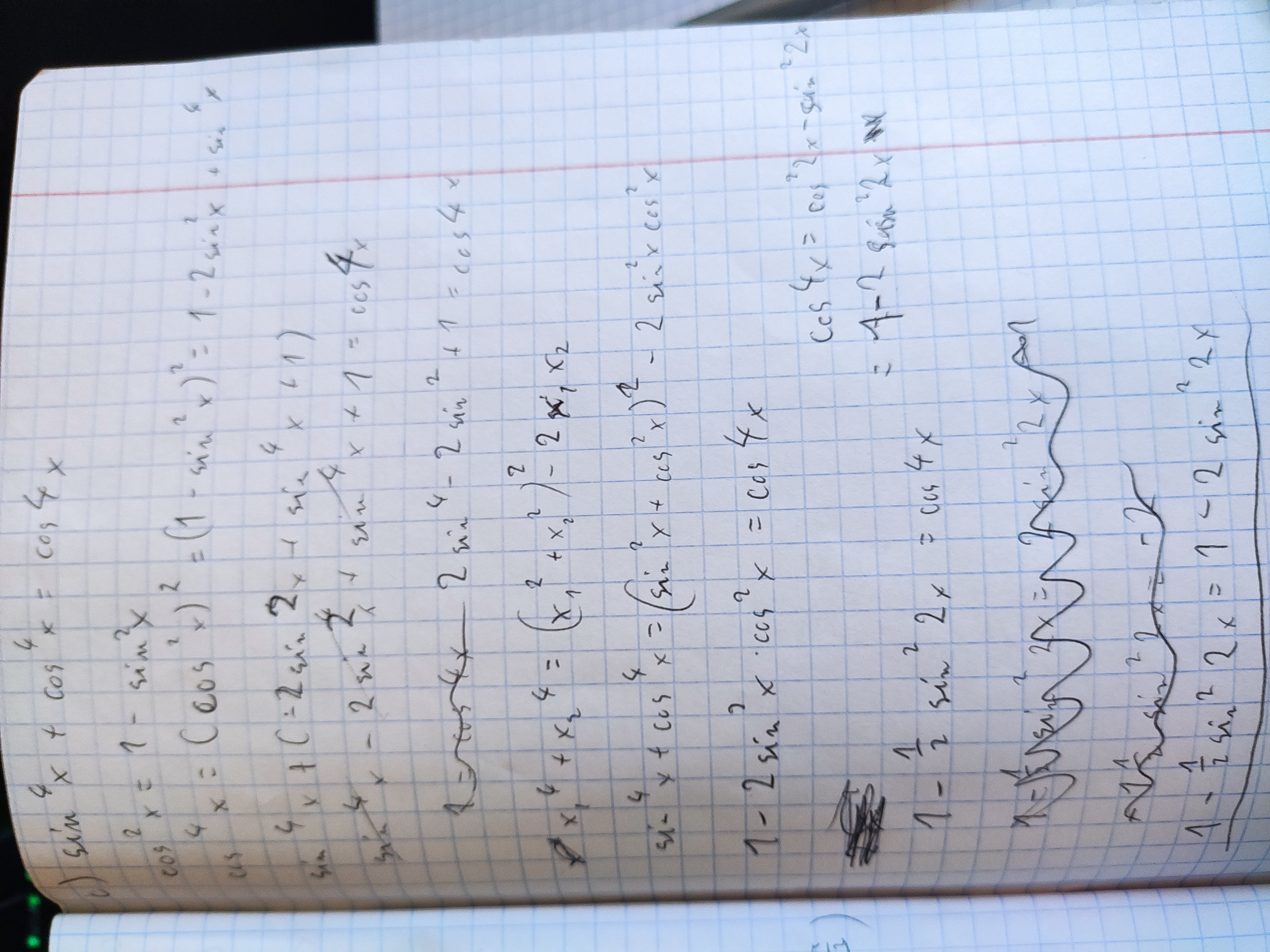
Co ja mam z tym zrobić?

matematyka trygonometria Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
viGor 30-10-2021 15:57
Zaproponuję Ci inny sposób na dokończenie tego:
Gdy rozbijesz sin^4 + cos^4[sin = a, cos = b; żeby było mi łatwiej pisać :P] na (a^2+b^2)^2 -2(ab)^2, to pomnóż obustronnie przez 2, żebyś mógł zrobić coś takiego: 1- 4sinxcosxsinxcosx, czyli mamy z tego coś takiego: 2 - sin^2(2x) = cos4x, potem zamień cos4x za pomocą wzoru(cos podwojonego kąta) na takie wyrażenie żeby występował tylko sinus. Wtedy się uda.  W razie problemów pisz :)