68/Prz.6.2

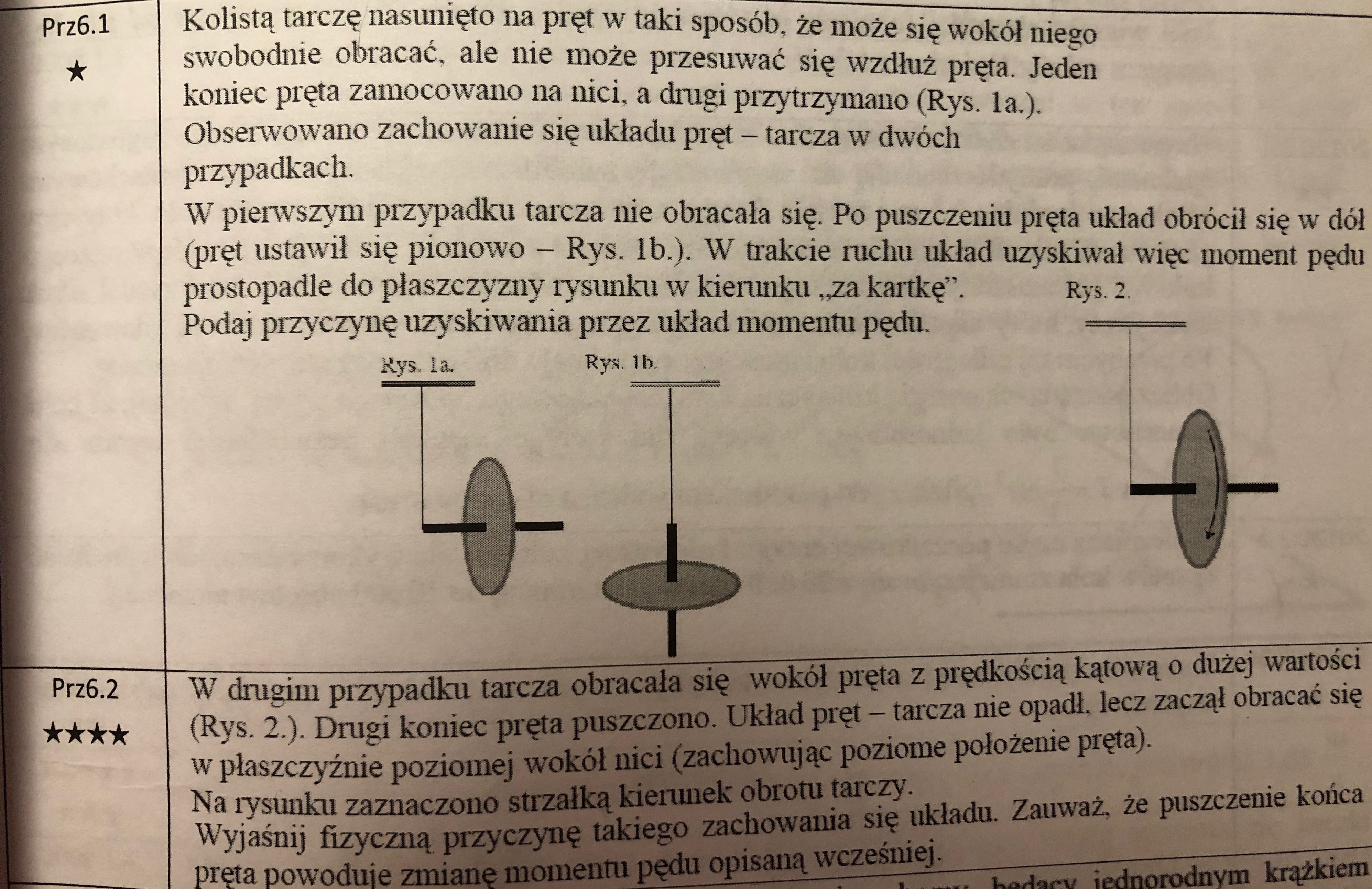
Puszczenie pręta sprawia, że działa na niego w pionie niezrównoważona siła ciężkości (wcześniej, gdy pręt był podtrzymywany, siłą ta byłą równoważona, więc można było powiedzieć, że w pionie efektywnie nie działała żadna siłą). W związku z tym pojawia się po puszczeniu pręta jakiś nowy niezrównoważony moment sił ciężkości. Zgodnie z drugą zasadą dynamiki w ruchu obrotowym (jej drugą wersją), pojawienie się wypadkowego momentu sił działającego na ciało powoduje zmianę jego momentu pędu:

$$ \frac{\Delta J}{\Delta t} = M => \Delta J = M \cdot \Delta t $$

A więc moment sił ciężkości względem punktu zaczepienia pręta do liny będzie zwrócony za rysunek, więc tak będzie zmieniał się moment pędu układu - stąd cały układ zacznie się obracać. Nie narysowałem tego, ale jedyna siłą jaka się tu pojawia to siłą ciężkości, no i jej moment.

Przy okazji tego zadania również nadmieniam, że nie może się ono w takiej postaci pojawić na maturze w 2022 roku.