2021.2
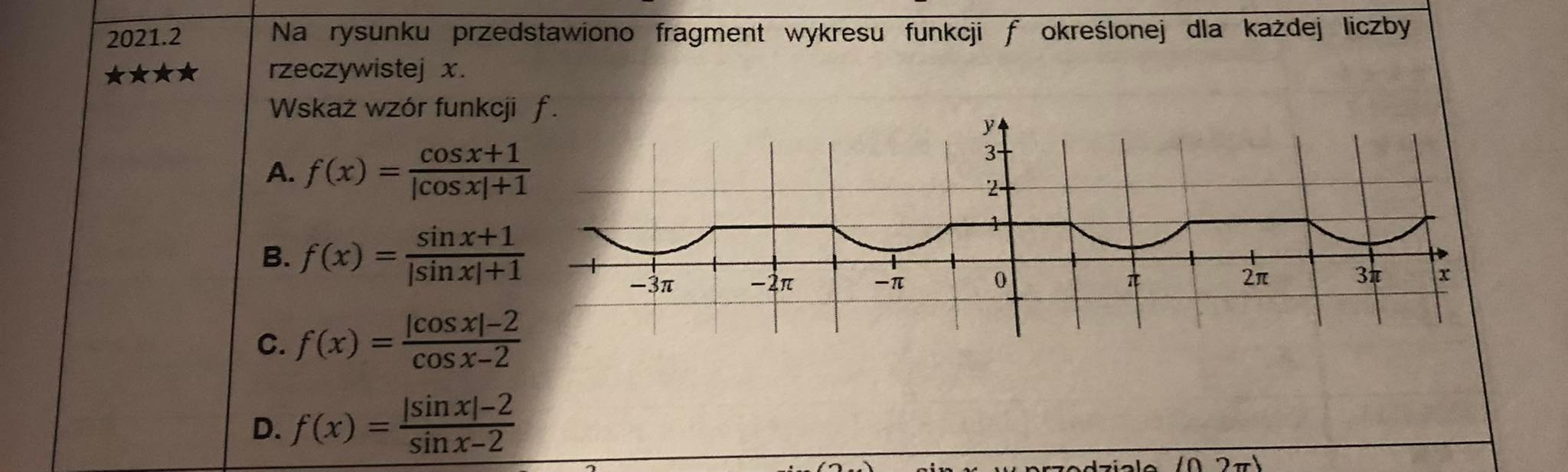
Ktoś mógłby mi wytłumaczyć jak podejść do tego zadania?
matematyka matura zbiór zadań zadanie maturalne Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
które opcje nam wypadają i dlaczego?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
W każdym wzorze f(x) mamy również wartość bezwzględną, którą należy uwzględnić.
Zgodnie z definicją:
Zatem w podpunkcie A sytuacja wygląda następująco:
f(x) = cosx + 1 / cosx + 1 dla cosx >= 0
f(x) = cosx + 1 / -cosx + 1 dla cosx < 0
co można skrócić do postaci:
f(x) = 1 dla cosx >= 0
f(x) = cosx + 1 / -cosx + 1 dla cosx < 0
W podpunkcie B:
f(x) = sinx + 1 / sinx + 1 dla sinx >= 0
f(x) = sinx + 1 / -sinx + 1 dla sinx < 0
co można skrócić do postaci:
f(x) = 1 dla sinx >= 0
f(x) = sinx + 1 / -sinx + 1 dla sinx < 0
W podpunkcie C natomiast:
f(x) = cosx - 2 / cosx - 2 dla cosx >= 0
f(x) = -cosx - 2 / cosx - 2 dla cosx < 0
co można skrócić do postaci:
f(x) = 1 dla cosx >= 0
f(x) = -cosx - 2 / cosx - 2 dla cosx < 0
Podpunkt D:
f(x) = sinx - 2 / sinx - 2 dla sinx >= 0
f(x) = -sinx - 2 / sinx - 2 dla sinx < 0
co można skrócić do postaci:
f(x) = 1 dla sinx >= 0
f(x) = -sinx - 2 / sinx - 2 dla sinx < 0
Mając wartość we wzorze funkcji już łatwo będzie nam porównać ją z podanym rysunkiem
W tym momencie wystarczy spojrzeć na wykresy funkcji cosx oraz sinx i sprawdzić gdzie przyjmuje wartości nieujemne
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Jako pierwszą rzecz warto zauważyć, że w miejscach gdzie funkcja jest stała i równa 1 musi zostać spełniony warunek licznik = mianownik. Po uwzględnieniu tej zależności wypadają nam już dwie opcje. Żeby wyłonić prawidłowy wzór z dwóch pozostałych sprawdzałem oba wzory przez zwyczajne podstawienie x i sprawdzenie czy wartość funkcji zgadza się z wykresem.