2016.11
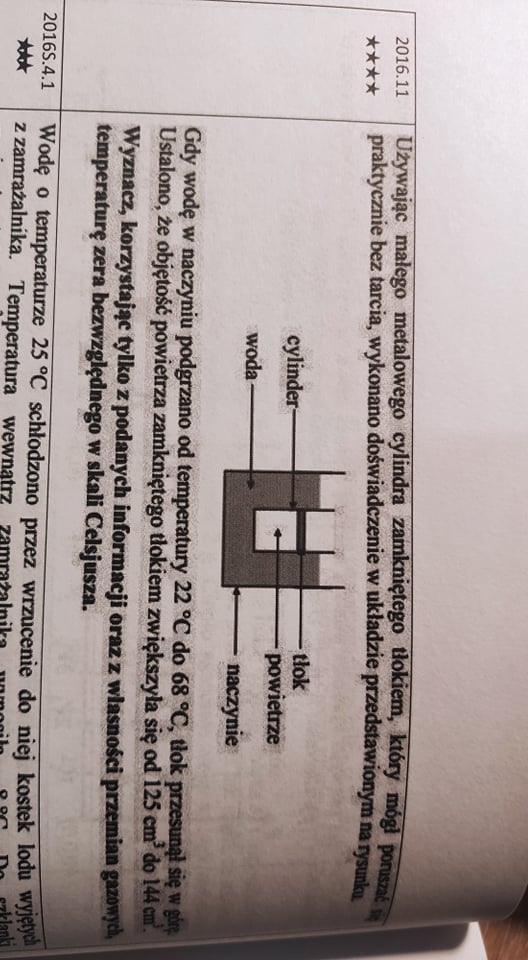
Od czego zacząć należy zacząć aby wyznaczyć zero bezwzględne w tym zadaniu? Proszę aby o początkowe założenia od czego należy wyjść.
termodynamika Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ale czy to jest możliwe żeby obliczyć to z równania Clapeyrona przecież jeśli dobrze rozumiem zero bezwględne jest wtedy kiedy V=0 wtedy również n=0, a więc cały wzór PV=nRT nam się wyzeruje.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Zgadza się - nie można sobie tego ot tak podstawić do równania Clapeyrona, bo faktycznie obie strony zwyczajnie się wyzerują (choć n nie będzie równe 0 wbrew temu co napisałeś, ale już V i T jak najbardziej). Dlatego właśnie zapisałem, że można skorzystać z równania Clapeyrona w takim sensie, że zauważymy, że zmiana objętości jest wprost proporcjonalna do zmiany temperatury: $$ \Delta V \sim \Delta T $$
Z treści zadania widzimy, że zmianie objętości równej 19 cm^3 odpowiada zmiana temperatury równa 46 K. No i na tej podstawie możemy obliczyć jaka zmiana temperatury odpowiada zmianie objętości o 125 cm^3 (z wartości 125 cm^3 do wartości 0 cm^3). To obliczenie możemy wykonać na przykład wykorzystując zwyczajnie proporcje.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Można to zrobić na dwa (a może i więcej) sposoby. W jednym z nich należałoby początkowo zauważyć, że mamy tu do czynienia z przemianą izobaryczną gazu (bo tłok może się swobodnie poruszać i nie działa na niego z zewnątrz żadna siła wymuszająca jego ruch). To byłoby nasze początkowe założenie - odpowiednie zapisanie równania dla tej przemiany (wynikające z równania Clapeyrona) doprowadzi nas do wyniku.
Drugi sposób polegałby ponownie na zauważeniu, że przemiana jest izobaryczna i użyciu równania Clapeyrona do stwierdzenia, że przyrost objętości jest wprost proporcjonalny do przyrostu temperatury, bo: $$ p \Delta V = nR \Delta T $$ i na tej podstawie można obliczyć dla jakiej temperatury objętość będzie zerowa.