zadanie domowe nr 9, zad 5
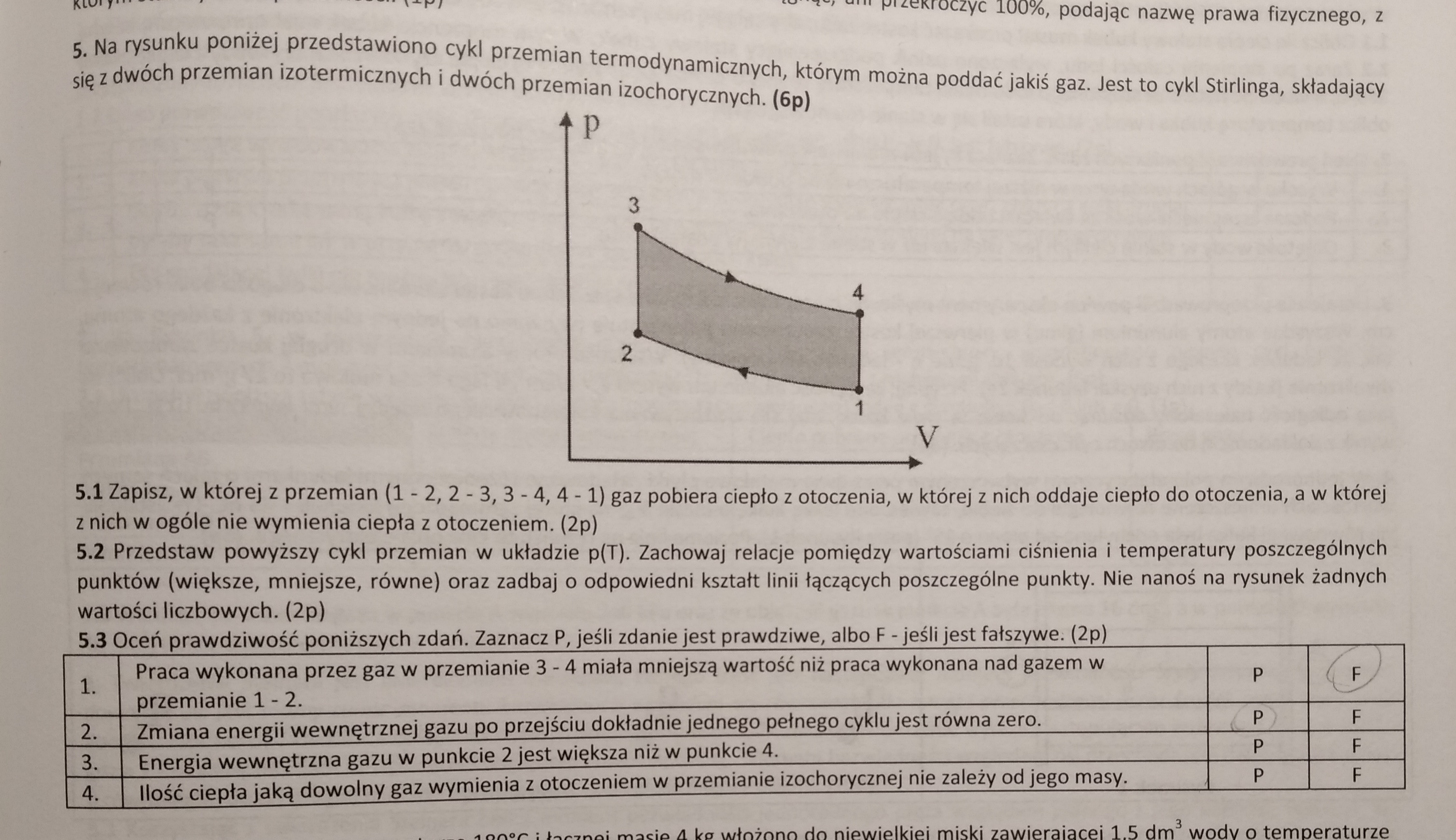
Proszę o wytłumaczenie całego zadania nr 5.
Fizyka termodynamika Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Dlaczego w podpunkcie 5.2 w cyklu, który trzeba było narysować, przedłużenia prostych przechodzących przez punkty 2 i 3 oraz punkty 1 i 4 mają przechodzić przez początek układu?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Dlatego, że zgodnie z równaniem Clapeyrona dostajemy: $$ p = \frac{nR}{V} \cdot T $$ a zatem zależność p(T) jest taka jak zależność y i x w funkcji liniowej typu y = a*x, a zatem wykres tej funkcji musi przechodzić przez 0 (tu wykres ów przechodziłby przez zero, gdybyśmy go przedłużyli).
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Wszystko jasne, dziękuję.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
5.1 - Dla przemiany izobarycznej i izochorycznej mamy wzory: $$ Q = n c \Delta T $$ trzeba więc zatem stwierdzić czy w tych przemianach temperatura wzrasta czy nie (a o tym powie nam zgodnie z równaniem Clapeyrona iloczyn pV - im on większy w danym punkcie, tym większa w tym punkcie temperatura). W przemianie izotermicznej musimy posłużyć się pierwszą zasadą termodynamiki, wiedząc, że zmiana energii wewnętrznej w takiej przemianie jest zerowa, zostaje zatem: 0 = Q + W. W każdej natomiast przemianie łatwo określimy znak pracy, wiedząc jak zmieniała się objętość gazu (jeśli objętość rośnie, to praca sił zewnętrznych W jest ujemna i na odwrót). Na tej podstawie poznamy znak ciepłą Q, więc będziemy wiedzieli czy zostało ono pobrane (wtedy Q > 0) czy oddane przez gaz.
5.2 - trzeba tu koniecznie wiedzieć jakimi krzywymi (lub prostymi) obrazowane są wszystkie przemiany w układzie p(T). To rzecz jasna wyciągniemy z równania Clapeyrona: pV = nRT.
5.3 - pp1: pamiętajmy, że pracę można obliczyć jako pole pod wykresem danej przemiany,
pp2: energia wewnętrzna jest proporcjonalna do temperatury. Po obejściu jednego cyklu gaz wraca do tego samego punktu, więc jego temperatura jest taka sama jak na początku, zatem energia wewnętrzna się nie zmienia.
pp3: jak wyżej, temperatura jest proporcjonalna do pV
pp4: korzystamy ze wzoru na ciepło w przemianie izochorycznej (nie ma tam co prawna bezpośrendio masy, ale jest liczba moli, która jest przecież proporcjonalna do masy gazu)