BG 400 wyśw. 19-11-2021 21:56

zad 1 zad 9 pr. domowa nr.9

Link do zdjęć zadań

Jak zrobić te zadania?

geometria płaska Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
blazej 20-11-2021 12:26

W zadaniu 1. narysuj sobie trójkąt równoramienny i podpisz boki, potem wyprowadź wzór na obwód (L=2x+2y), po podstawieniu 32 za L wylicz x lub y (założenia: x>0, y>0). Na końcu z twierdzenia Pitagorasa za x^2 lub y^2 podstawiasz to, co ci wyszło i liczysz pozostałe boki oraz pole.

 

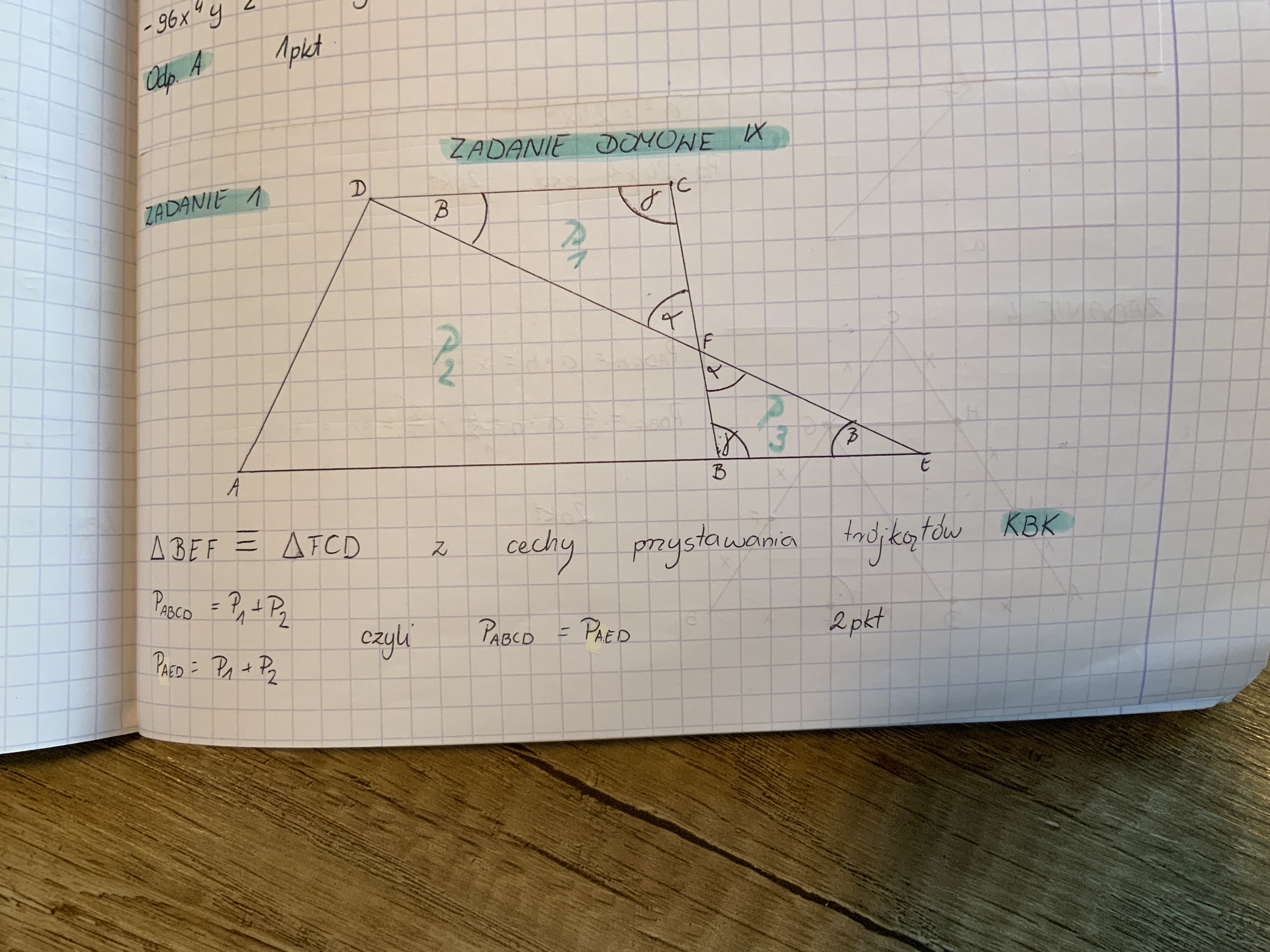
W zadaniu 2. zauważ, że trójkąty FCD i EFB są przystające na zasadzie kąt-bok-kąt (z treści zadania: |CF|=|FB|), wiedząc to, można zapisać, że pola ABFD+FCD są równe sumie pól ABFD+EFB, ckd.

Ola 19-01-2022 12:52