2016C.8.2

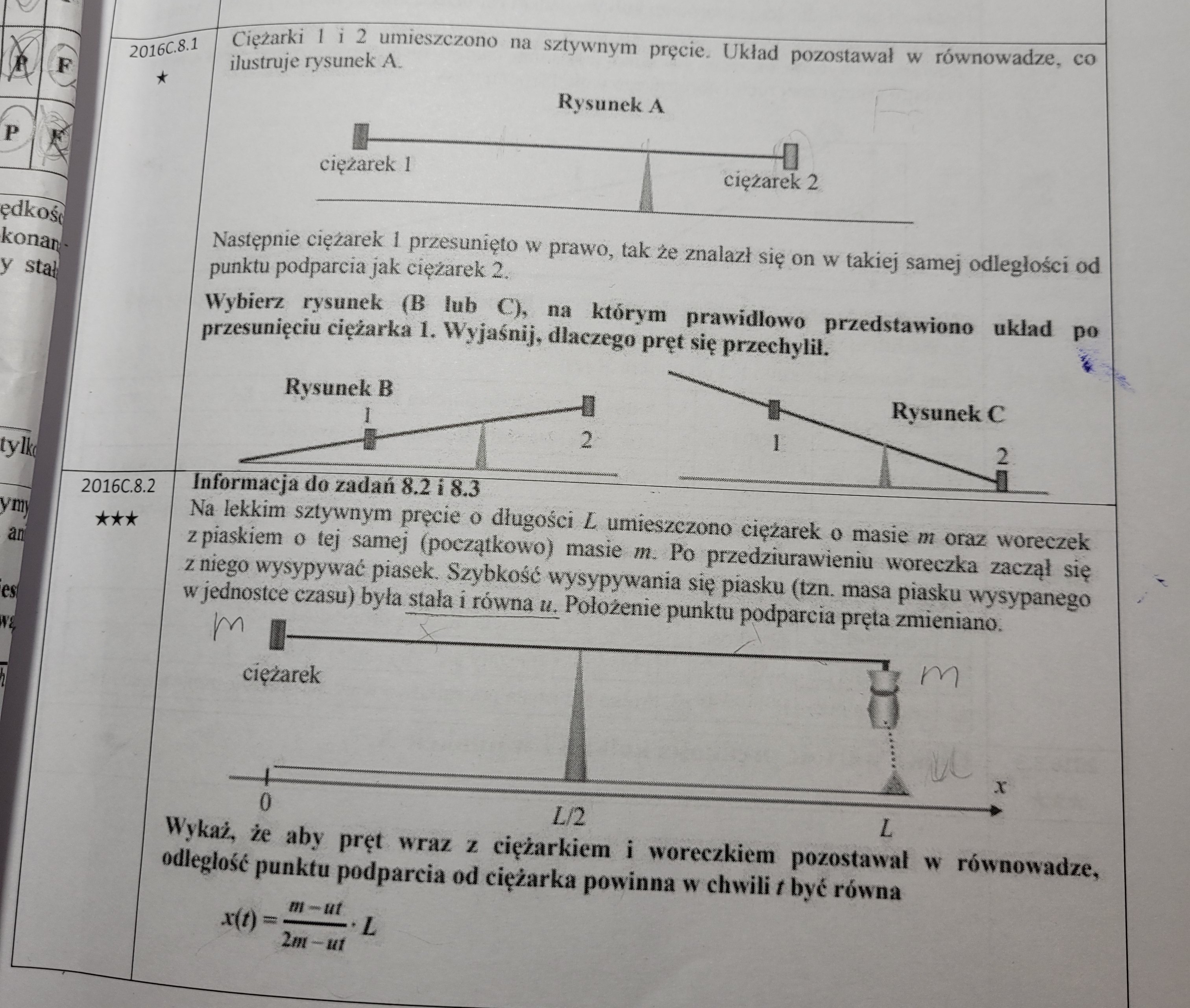
Należy tu pamiętać, że aby układ pozostawał w równowadze, to momenty sił wynikających z ciężarów ciężarka i worka z piaskiem muszą się równoważyć. Co więcej, skoro szybkość wysypywania się piasku to u, to masę worka z piaskiem w zależności od czasu można zapisać jako m - ut (u to masa wysypywanego piasku w jednostce czasu, więc jak pomnożymy ją przez czas to dostaniemy ut, czyli masę wysypanego piasku po czasie t). No i teraz trzeba przyrównać wspomniane momenty dla czasu t, przyjmując, że odległość podpory od ciężarka to zgodnie z poleceniem x. Dostajemy zatem: $$ xmg = (L - x) \cdot (m - ut) \cdot g $$ i stąd wyprowadzimy wzór na x.