Kiełbasa 609/106

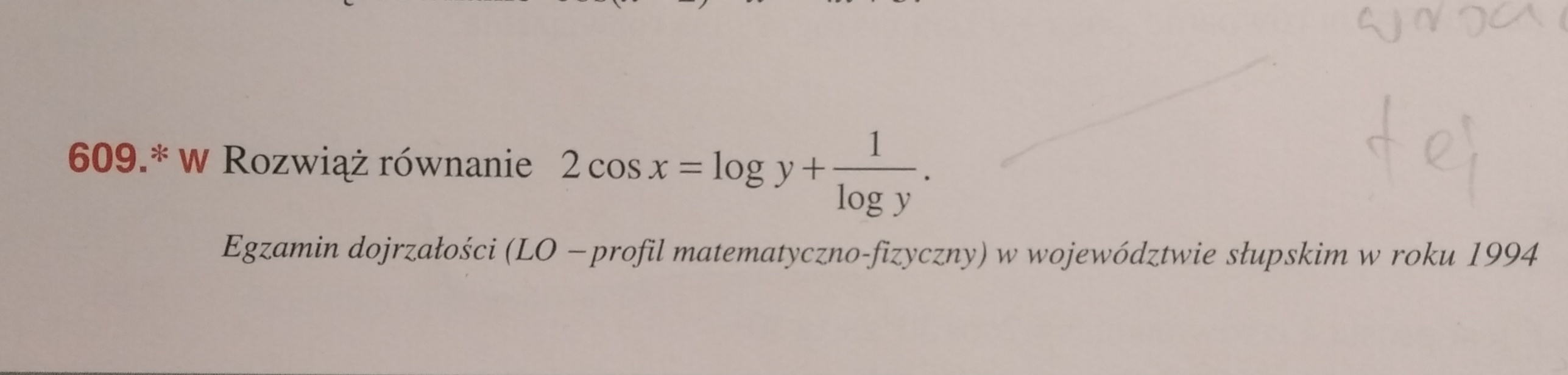
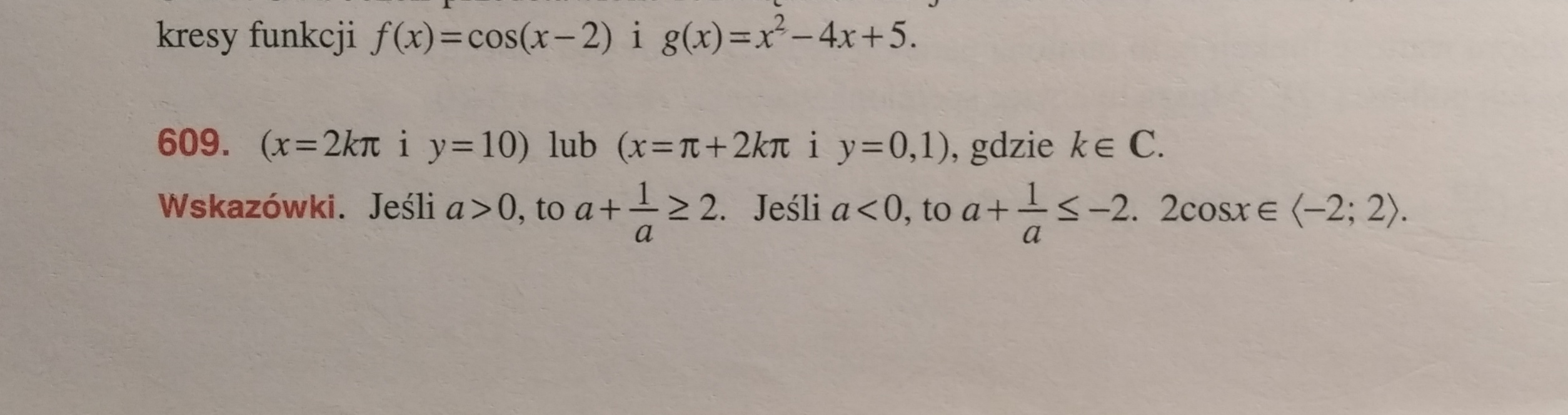
Nie rozumiem z czego wynika drugie równanie we wskazówkach (dla a<0). Pierwsze jeśli się nie mylę wynika z (a-1)^2 >= 0. Domyślam się, że to drugie wyznacza się analogicznie, tylko czegoś nie rozumiem. Według mnie powinno być bez minusa przy dwójce (tak jak na zdjęciu zeszytu).
Trygonometria logarytmy rozszerzenie Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Jakie jest najlepsze podejście do tego zadania? Na maturze jakbym walczył z takim zadaniem to wystarczyłoby napisać te dwa wzory, które są we wskazówkach dla a>0 i a<0 i dopisać, że wynikają one z wykresu funkcji f(x) = x + 1/x? (no i rozwiązać oczywiście). Czy może lepiej wyprowadzić je z (a + 1)^2 i (a - 1)^2 ?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Polecałbym wyprowadzić -> szybciej i pewniej.
Dodatkowo: tego, że suma dowolnej liczby dodatniej i liczby do niej odwrotnej jest nie mniejsza niż dwa nie trzeba specjalnie udowadniać gdyż jest to powszechnie wykorzystywane twierdzenie.
Poniżej jeszcze rozwiązanie aby rozwiać wątpliwości:

- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Twoje rozwiązanie jest poprawne.
Dla a<0 nierówność a+1/a<=0 jest zawsze spełnione, natomiast tą nierówność również można zawęzić:
Spójrz dodatkowo na wykres funkcji: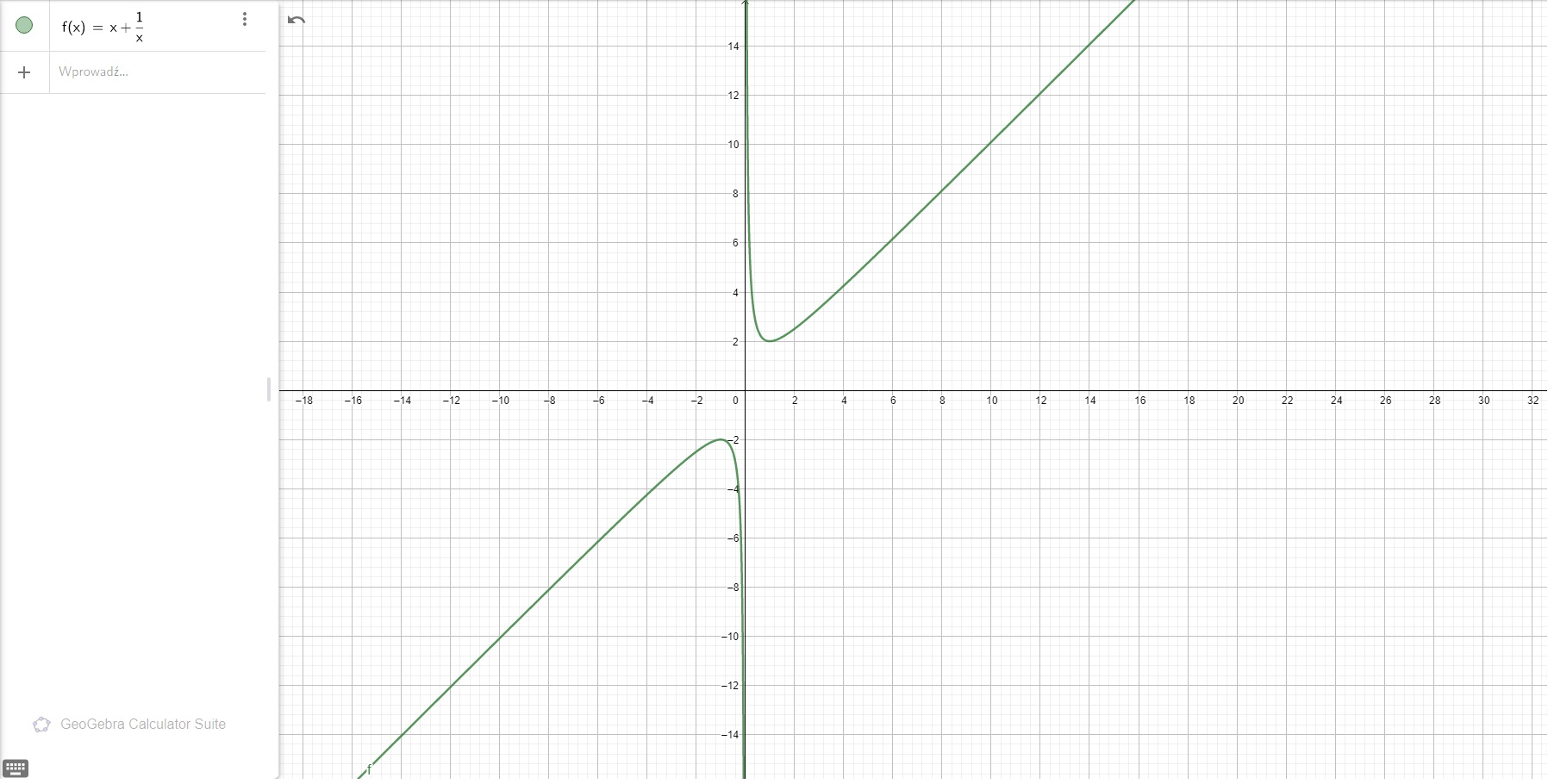
W skrócie twoja nierówność jest prawdziwa - natomiast nierówność w książce jest również prawdziwa :)