mm 452 wyśw. 01-12-2021 22:34

2016C.3


Cześć, zrobiłam to zadanie za pierwszym razem dobrze i  wyszedł mi poprawny wynik, ale potem zaczęłam się zastanawiać, dlaczego tak właściwie siły wyporu w obu przypadkach są sobie równe, skoro łodzie poruszają się ruchem jednostajnym prostliniowym przez co ich siły wypadkowe muszą być równe 0. Rozpisałam na zdjęciu o co mi dokładniej chodzi. Z góry dzięki za pomoc, pozdrawiam!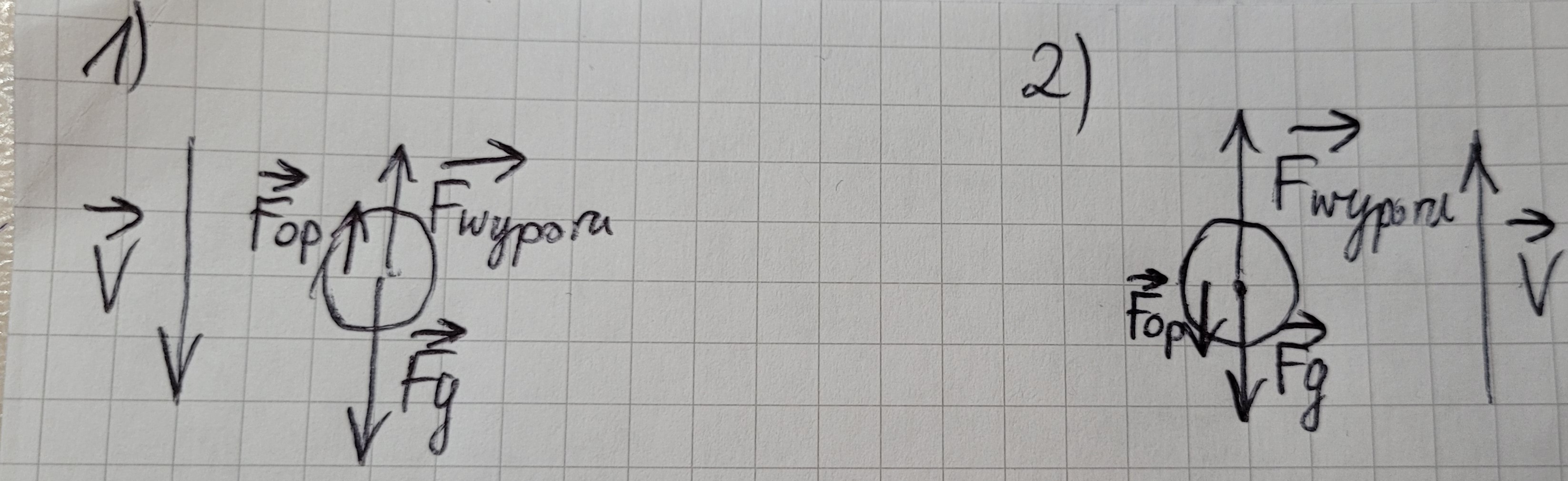

Hydrostatyka Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
s.gugula 03-12-2021 10:24

Siły wyporu są sobie równe, ponieważ siłą wyporu zależy tylko od gęstości cieczy, w której zanurzone jest ciało (ta się nie zmienia), od przyspieszenia ziemskiego (też się nie zmienia) i od objętości zanurzonego ciała (to też się tu nie zmienia): $$ F_{wyporu} = \rho \cdot g \cdot V_{zan} $$

mm 04-12-2021 12:44

Dzień dobry, a dlaczego mówimy, że w obu przypadkach ta łódź podwodna porusza się ruchem jednostajnym, skoro siły wyporu i siły oporu wody są takie same zarówno w pierwszej i drugiej sytuacji a siły ciężkości się przecież zmieniły. Pozdrawiam.


s.gugula 04-12-2021 14:15

To, że w obu przypadkach mamy ruch jednostajny wiemy z treści zadania. Żeby w obu przypadkach ów ruch jednostajny się pojawił, to w obu przypadkach działające na siły ciało muszą się zrównoważyć. Rzeczywiście siłą oporu i wyporu są w obu przypadkach takie same, ale siła oporu działa raz w górę a raz w dół i okazuje się, że jeśli siłą ciężkości zmniejszy się w odpowiedni sposób, to w obu przypadkach możemy uzyskać równowagę sił. Na tej zresztą podstawie należy obliczyć siłę oporu.

adaganko 13-12-2021 12:54

A więc z równowagi sił w obydwu przypadkach wynika, że F oporu są jednakowe w obydwu przypadkach?

s.gugula 13-12-2021 13:15

To że sił oporu co do wartości są w obu przypadkach jednakowe można wywnioskować już z samego faktu, że w obu przypadkach łódź porusza się ruchem jednostajnym z tą samą wartością prędkości. O sile oporu wiemy bowiem, że jest ona zależna właśnie od prędkości, skoro jej wartość w obu przypadkach jest taka sama, to wartość siły oporu również. Równowaga sił sprawia natomiast, że możemy tę wartość dodatkowo obliczyć (wiedząc jak wygląda wzór na siłę wyporu i jaka jest siła ciężkości).