san2 464 wyśw. 02-01-2022 14:39

Zadanie domowe nr 12, 6b/349


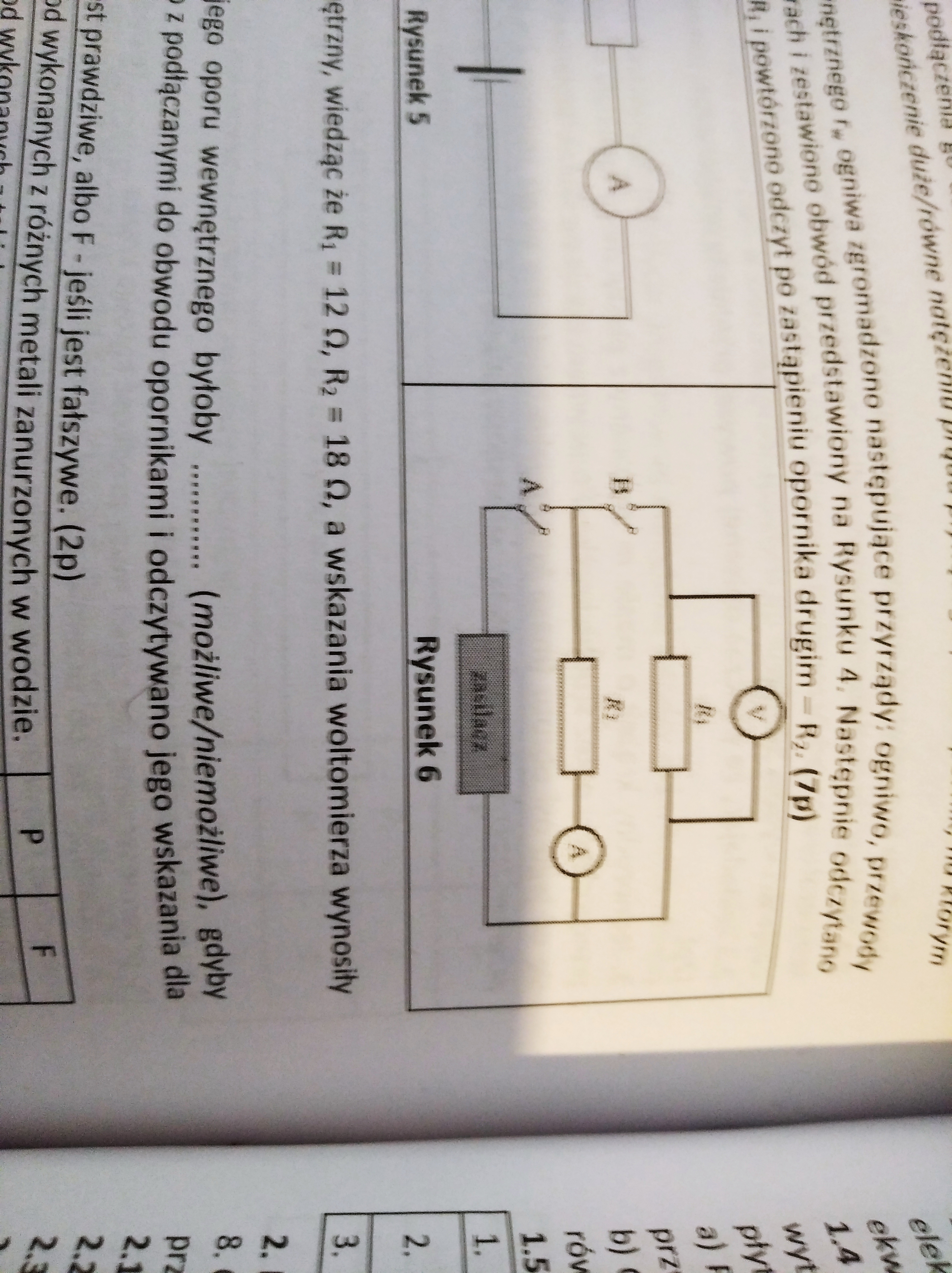
Przy obu otwartych kluczach natężenie tego prądu wynosiłoby U/R2, gdzie U jest napięciem pochodzącym z zasilania i nie zmienia się. Po otwarciu klucza B cała górna gałąź obwodu zostaje z niego wyłączona, ale nie wpływa to na napięcie na oporniku R2, gdyż napięcie źródła U pozostaje stałe, a zatem natężenie na nim (mierzone przez amperomierz) wciąż byłoby równe U/R2. Dlaczego więc natężenie prądu wskazywane przez amperomierz przy zamkniętym kluczu A, a otwartym B wzrasta według klucza odpowiedzi?

Fizyka zbiór zadań prąd elektryczny Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
s.gugula 03-01-2022 13:02

Kluczowy jest tutaj fakt, że uwzględniamy (jest to nawet podkreślone w treści zadania) opór wewnętrzny zasilacza (oznaczmy go jako r). Moglibyśmy go nawet sobie narysować w tym obwodzie jako taki opornik połączony szeregowo ze źródłem napięcia (zasilaczem). Można teraz zauważyć, że opór zastępczy całego układu oporników R1, R2 i r jest przy obu zamkniętych kluczach inny niż w sytuacji opisanej w przypadku B - w związku z tym w całym obwodzie popłynie na pewno prąd o innym natężeniu. Można dokładnie obliczyć ów prąd w obu przypadkach wykorzystując prawa Kirchhoffa. W przypadku gdy oba klucze są zamknięte dostaniemy: $$ I_2 = \frac{E}{r + R_2 + \frac{r R_2}{R_1}} $$ gdzie E to siła elektromotoryczna zasilacza, natomiast w przypadku otwartego klucza B dostaniemy: $$ I_2 = \frac{E}{r + R_2} $$ i widać że faktycznie ta druga wartość jest większa niż pierwsza (mniejszy mianownik). Więc faktycznie tak jak wspomniałem na początku kluczowy jest fakt, że musimy uwzględnić opór wewnętrzny zasilacza. Gdyby można było go pominąć, to faktycznie w obu przypadkach natężenie byłoby takie samo.