KS 314 wyśw. 16-01-2022 15:52

diament 2016/2017

Na bocznej powierzchni klina nachylonej pod kątem α do poziomu znajduje się klocek o masie m = 0,2 kg. Współczynniki tarcia statycznego i kinetycznego są sobie równe i wynoszą f = 1, dla tarcia między klockiem a klinem. Na skutek tarcia klina o podłoże, klin pozostaje cały czas w spoczynku! Dla jakiej minimalnej wartości kąta α klocek będzie się zsuwał po powierzchni klina? Następnie oblicz siłę tarcia klocka o klin, siłę tarcia klina o podłoże oraz wartość wypadkowej siły oddziaływania klocka na klin, dla dwóch przypadków: A/ kąt α=α1=30°, B/ kąt α=α2=60°. Zrób rysunek z zaznaczeniem sił oddziaływania klocka na klin.

Jeśli nieruchomy klocek znajduje się na klinie pod kątem a=30, siłę tarcia można zapisać jako T=Fx=mgsina,
można jednak wykorzystać w tym przypadku inny zapis, czyli T=Fnf= mgcosaf=mgcosa (tu f=1) Dalej: mgcosa=mgsina co daje cosa=sina, a to jest sprzeczne. Gdzie jest błąd?

Tarcie klin Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
s.gugula 17-01-2022 14:26

Skąd wziąłeś pierwszy wzór na tarcie, mianowicie T = Fx = mg*sin(alfa)?  Tam właśnie ma być cos(alfa) i wtedy nie ma żadnej sprzeczności :)

KS 17-01-2022 20:13

Ten pierwszy wzór jest z 1zd Newtona, jeśli ciało pozostaje w spoczynku to składowa pozioma (pozioma dla klocka) musi równoważyć tarcie.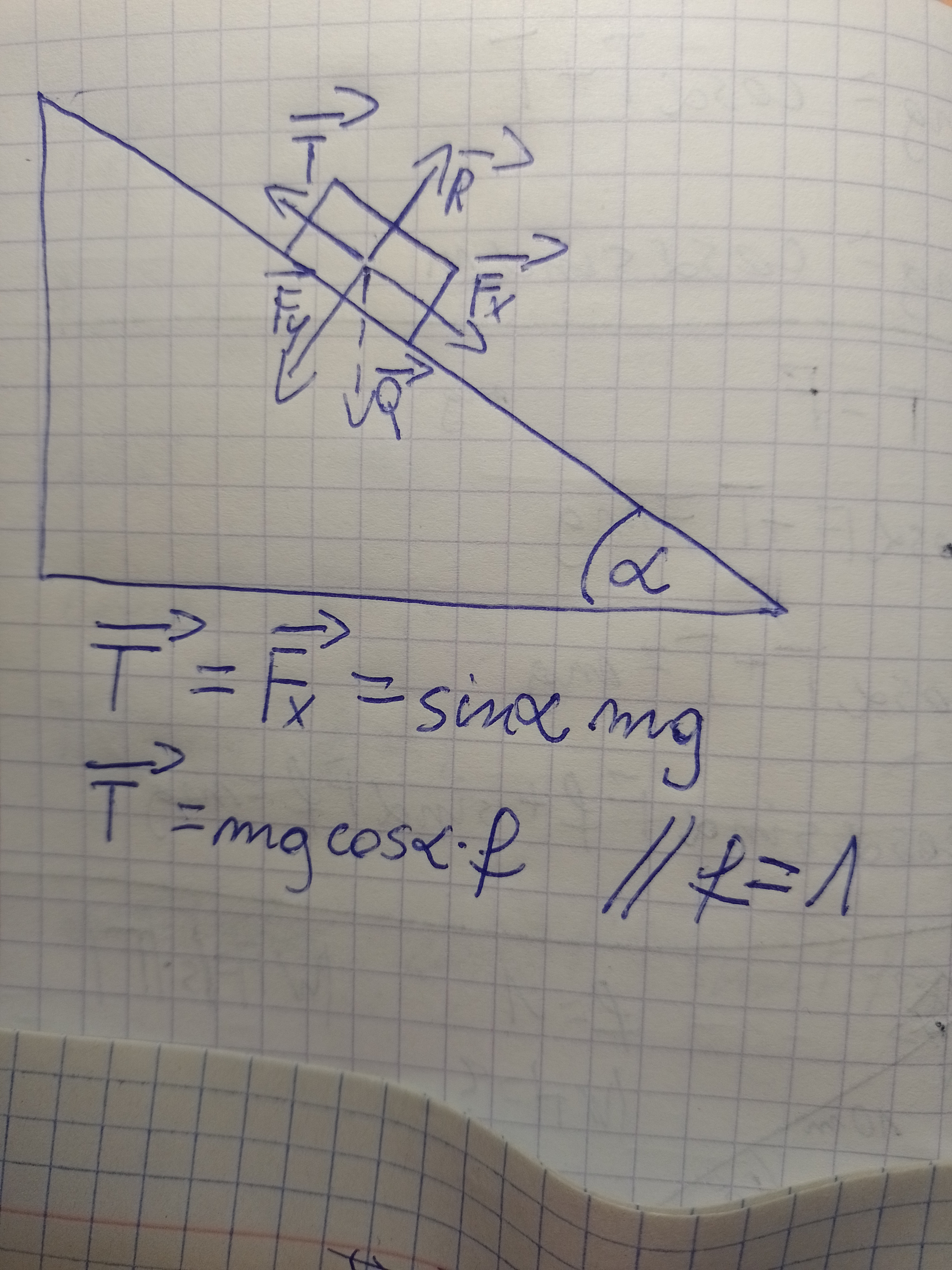

s.gugula 18-01-2022 11:49

Przepraszam, bo faktycznie nie doczytałem wcześniej, że to jest dla klocka w spoczynku. Ale tu z kolei pojawia się kolejny ważny szczegół dotyczący tarcia statycznego - bo z takim mamy do czynienia. Mianowicie tylko maksymalna wartość tarcia statycznego jest równa f*Fn, natomiast jeśli nie bierzemy pod uwagę jego maksymalnej wartości (czyli tej w sytuacji granicznej), tylko każdą inną, to tarcie statyczne jest mniejsze od wartości f*Fn, więc nie możemy go zapisać jako f*mg*cos(alfa). Zostaje jedynie możliwość zapisania go jako Fx = mg*sin(alfa), tak jak to zrobiłeś i znika nam pozorna sprzeczność.