2017.2.2

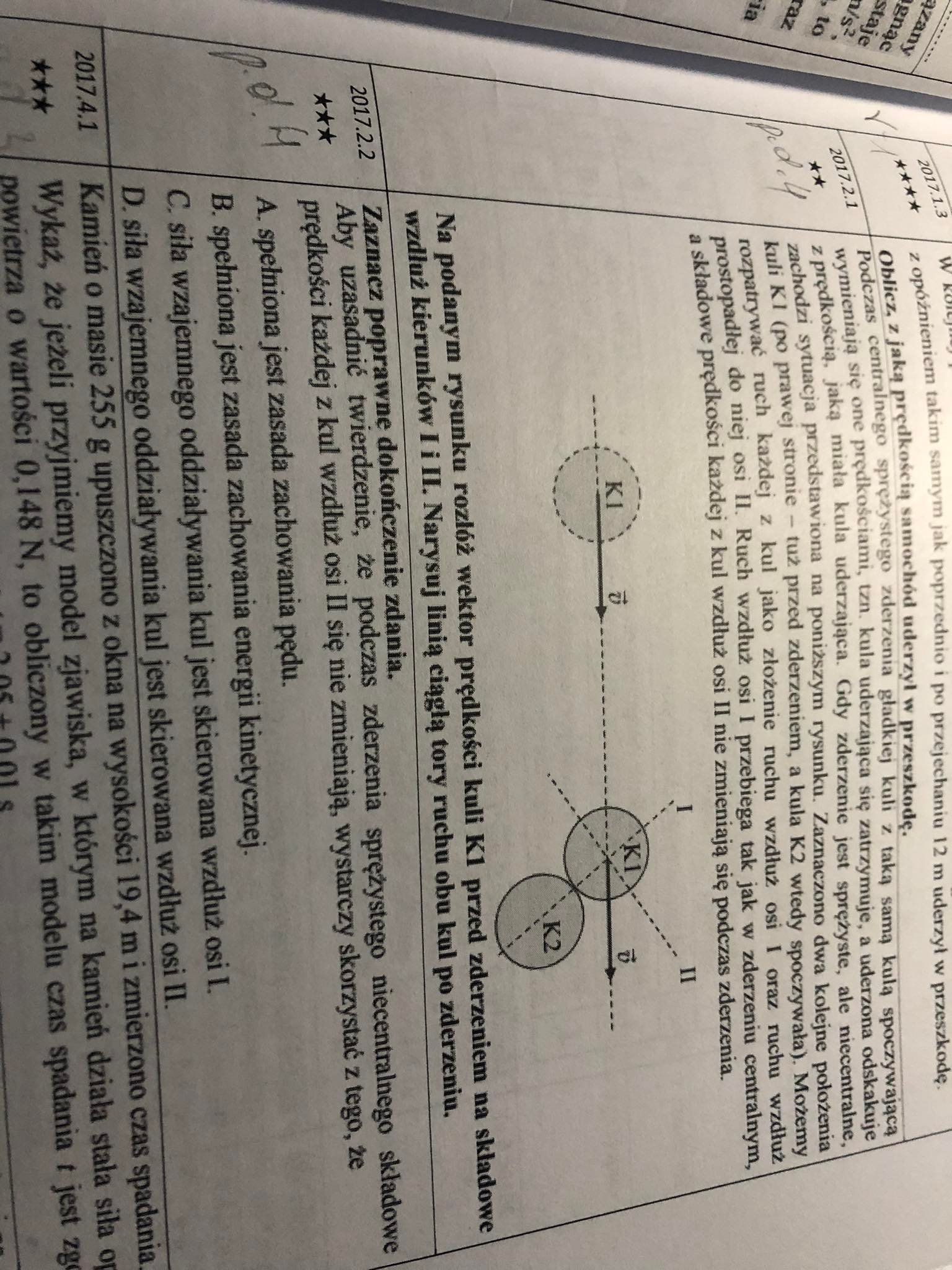
Odpowiedź C jest poprawna, ponieważ z drugiej zasady dynamiki (jej drugiej postaci) wiemy, że siła powoduje zmianę pędu w czasie: $$ F = \frac{\Delta p}{\Delta t} $$ a ponieważ w tym przypadku siła oddziaływania pomiędzy kulami faktycznie działa wzdłuż prostej I (na tej prostej leżą środki tych kul), to oznacza to, że ta siła powoduje zmianę tych składowych pędów tych kul, które leżą w kierunku tej prostej. Tymczasem prosta II jest prostopadła do prostej I, a zatem siła działająca w kierunku prostej I nie ma żadnego wpływu na składowe pędów (a co za tym idzie prędkości) tych kul wzdłuż osi II.

Warto jednocześnie zwrócić uwagę na fakt, że sama zasada zachowania pędu by tutaj nie wystarczyła (choć ona jest oczywiście spełniona), bo ona mówi jedynie o tym, że całkowity pęd układu jest zachowany, natomiast do zauważenia, że wzdłuż osi II te składowe się nie zmieniają konieczna jest wiedza o tym, jak ułożona jest wspomniana siła oddziaływania.