próbna nowa era 2022
Czy mogę prosić o wyjaśnienie odpowiedzi do zadania?
fizyka Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
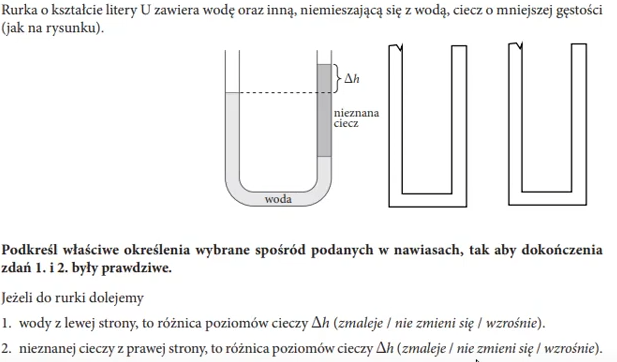
W takim razie czy dobrze rozumiem, że dolewając wody z lewej
strony to (po wyprowadzeniu delta h) w liczniku uzyskujemy (gęstość wody*(x1+y)
gdzie y jest to wysokość słupa dolanej wody. Stąd wychodzi, że ta różnica
będzie teraz większa niż wcześniej?
I analogicznie do drugiego podpunktu? czy wciąż coś mieszam?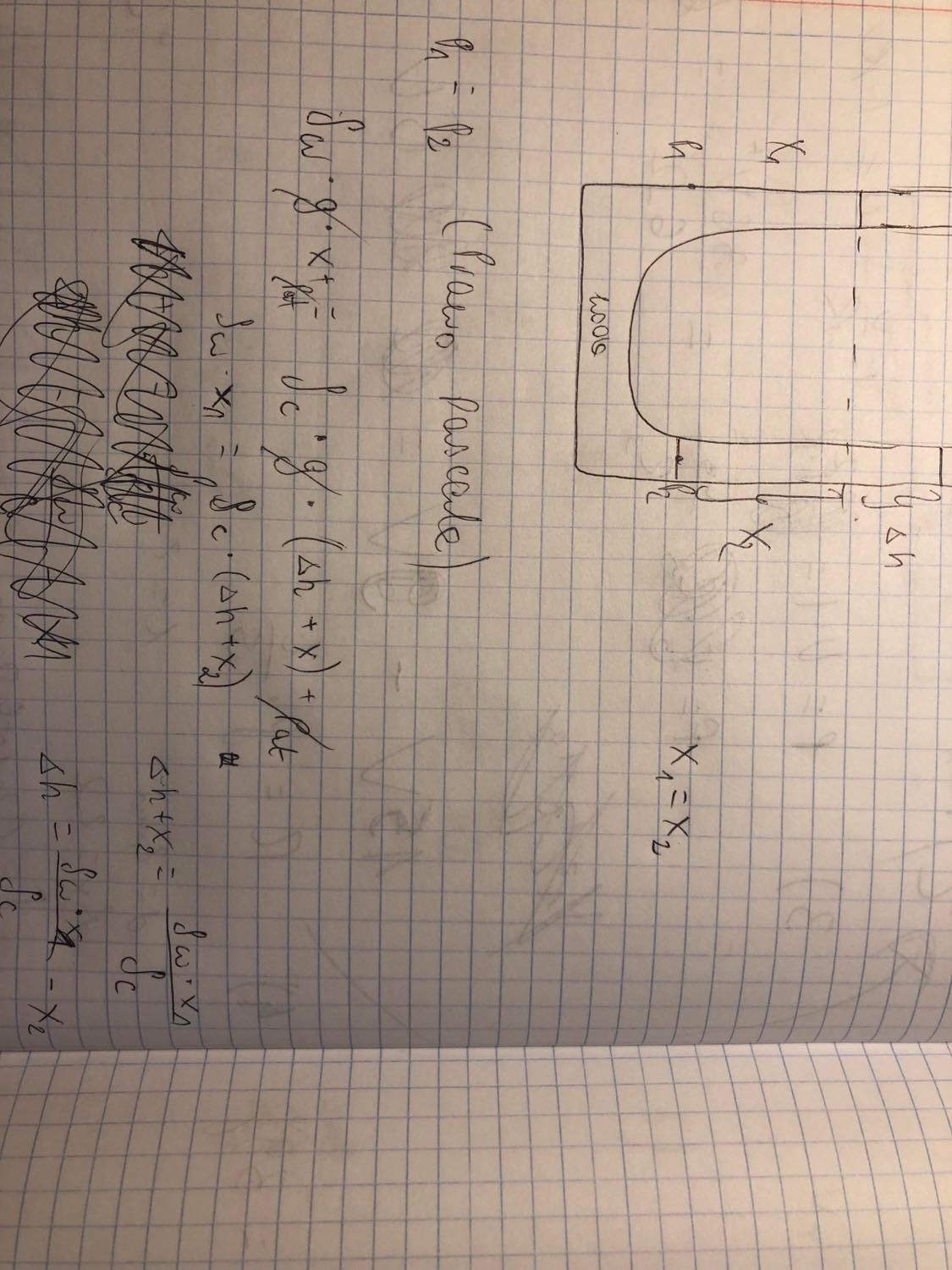
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Wyprowadzenie, które przedstawiłaś na zdjęciu jest dobre, natomiast nie można raczej wnioskować z niego, że po dolaniu np. wody w ilości y do lewej strony naczynia wysokość słupa wody ponad przyjętym poziomem w lewym ramieniu to będzie x1 + y, bo przecież wysokość, na której znajduje się ten przyjęty poziom może się zmienić. Dlatego w moim poprzednim komentarzu sugerowałem, aby jako x oznaczyć sobie wysokość słupa nieznanej cieczy. Wtedy powinniśmy dojść do następującego wzoru na deltah: $$ \Delta h = \frac{x (\rho_w - \rho_c)}{\rho_w} $$ i stąd łatwo już wywnioskować co się stanie jeśli dolejemy wody (nie zmienia się wtedy x, więc nie zmienia się deltah) oraz co się stanie gdy dolejemy trochę nieznanej cieczy (rośnie x).
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Można to wyprowadzić wykorzystując prawo Pascala. najlepiej jest zapisać równość ciśnień hydrostatycznych na tej samej wysokości w wodzie - wysokość, którą najlepiej przyjąć to ta, na której woda styka się w prawym ramieniu z nieznaną cieczą. Oznaczając np. wysokość słupka nieznanej cieczy przez x, możemy w zależności od tej wysokości x oraz gęstości wody i nieznanej cieczy wyznaczyć wielkość deltah. Na tej podstawie możemy stwierdzić co się stanie gdy dolejemy trochę wody, a co gdy dolejemy trochę nieznanej cieczy (zobaczymy jak zmienia się deltah). W razie dalszych pytań proszę śmiało pisać.