Kiełbasa cz.II 204

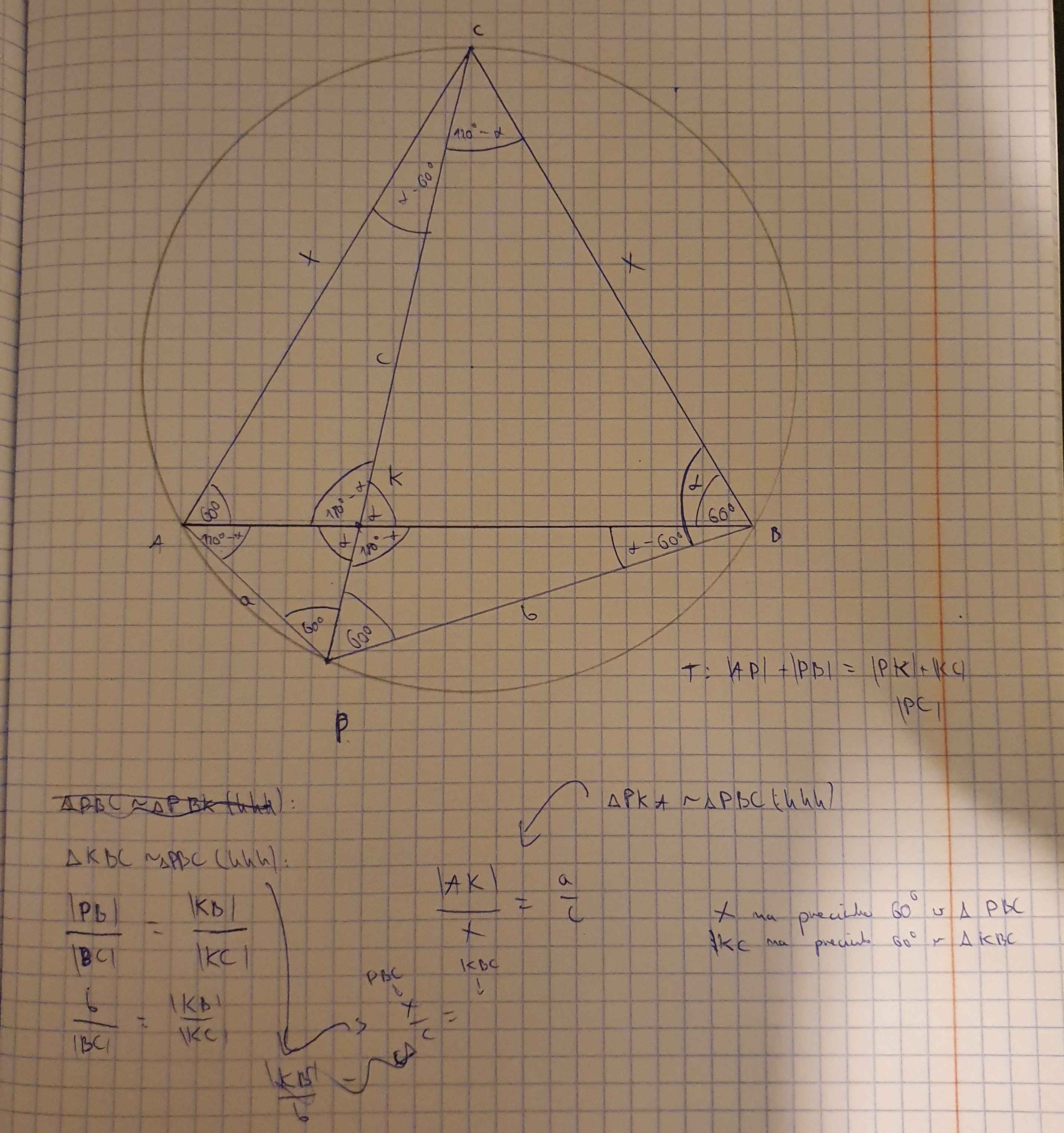
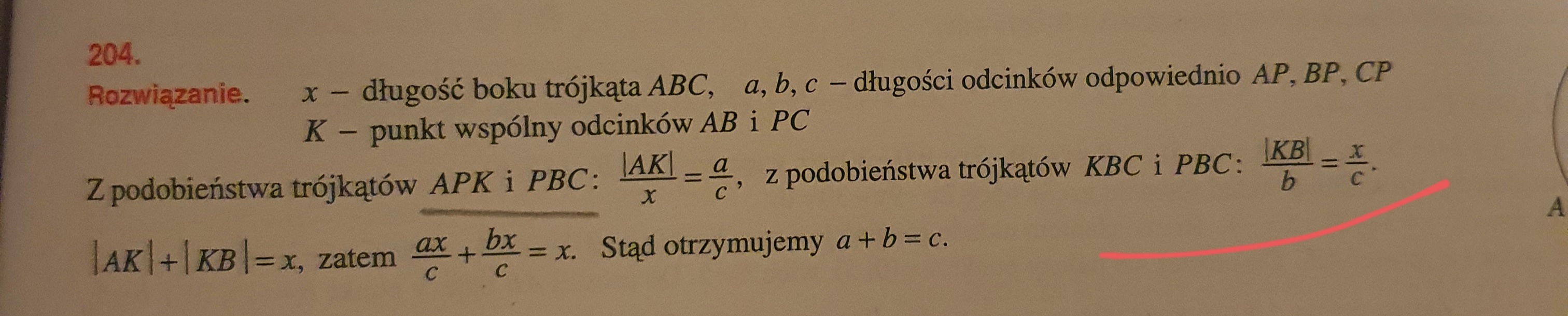
Cześć, podobieństwo odpowiednich trójkątów można w miarę łatwo odnaleźć patrząc na kąty, jednak zupełnie nie rozumiem skąd biorą się te stosunki z rozwiązania. Na swojej kartce po prawej na dole zapisałem co jeść gdzie w trójkącie, a w odpowiedziach mamy np. |KB|/b = x/c; x oraz c należą do PBC, ale b nie należy do KBC, a KB już tak.
Skąd wzięły się te stosunki? Próbowałem to jakoś orientować wdg kątów, ale i tak nie zauważam tego co w odpowiedziach
Okrąg podobieństwo Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Czyli wniosek z tego taki, że mogę dzielić bok z jednego trójkąta, przez bok z drugiego trójkąta, tylko potem pozostałą cześć równości muszę dobrać tak, żeby te boki też sobie odpowiadały? (tak jakby przyrównał k=k, tylko że jedno k "stwarzam" w inny sposób niż to drugie?)
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tak, proporcje można tworzyć na różne sposoby.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Stosunki wzięły się z podobieństwa dwóch trójkątów KBC i PBC.
|KB|/b oznacza, że wzięto bok |KB| trójkąta KBC i podzielono go przez odpowiedni bok (leżący na przeciw tego samego kąta tylko w trójkącie do którego jest podobny, czyli bok "b" w trójkącie PBC.
Analogicznie =x/c , wzięto bok "x" z trójkąta KBC (leży on na przeciwko kąta alfa). Dzielimy przez odpowiedni bok trójkąta PBC (czyli "c").
Jest to klasyczne wykorzystanie podobieństwa dwóch trójkątów.