2020.3.3

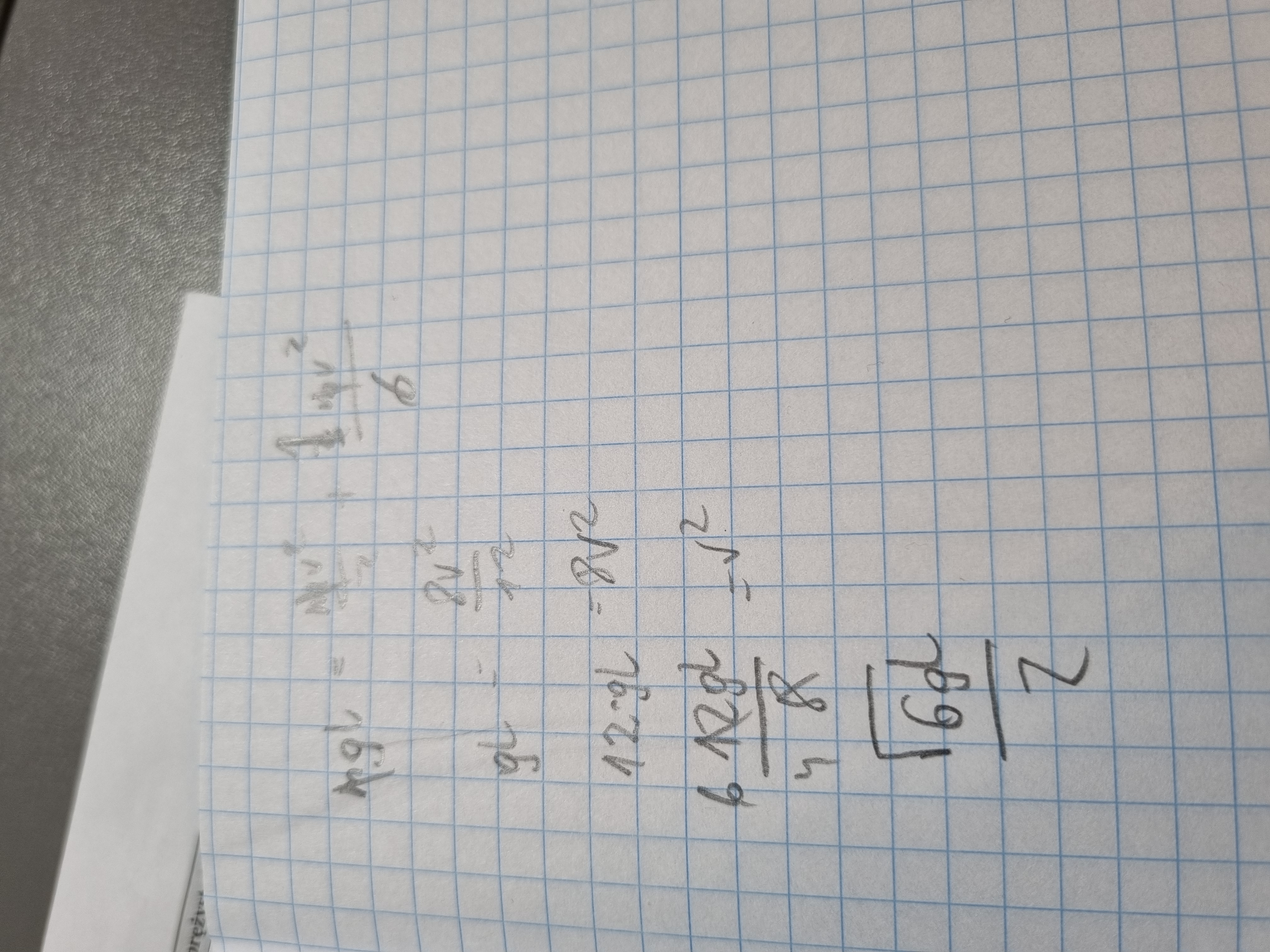
Obliczenie jest niestety niepoprawne. Sposób na wykorzystanie zasady zachowania energii jest dobry, natomiast niestety błędnie wpisane są te energie. Na początku pręt faktycznie posiadał wyłącznie energię potencjalną, przy czym w przypadku bryły sztywnej patrzymy na to na jakiej wysokości znajduje się jej środek masy. A zatem poziom zerowy najlepiej jest przyjąć sobie w połowie długości pręta, gdy ten już wisi pionowo. Wówczas początkowa energia potencjalna to m*g*(l/2). Jeśli chodzi o energię końcową, to bryła wykonuje jedynie ruch obrotowy względem osi obrotu (środek masy nie wykonuje żadnego dodatkowego ruchu postępowego względem osi obrotu), w związku z czym energia końcowa to będzie energia kinetyczna w ruchu obrotowym, a zatem I*w^2/2, gdzie w to prędkość kątowa, którą można powiązać z prędkością liniową poprzez wzór: v = w*(l/2), bo l/2 to promień okręgu, po którym porusza się środek masy pręta. A zatem dostajemy równanie: $$ mg \frac{l}{2} = \frac{I \omega^2}{2} $$ do niego należy wrzucić omegę ze wzoru zapisanego wcześniej i wykorzystać fakt, że I = 1/3 ml^2 i powinno wyjść v = 1/2 * pierw(3gl)