próbna nowa era 2017 zad. 9.3 i 9.4

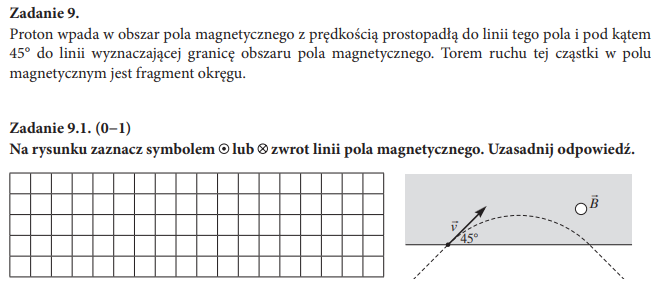
9.3: w takiej sytuacji zawsze należy zauważyć, że siłą Lorentza pełni rolę siły dośrodkowej, zatem: qvB = mv^2/r, a stąd możemy wyznaczyć promień okręgu zakreślanego przez proton: r = mv/qB. Skoro mamy do czynienia z ruchem po okręgu, to możemy zapisać wartość prędkości w takim ruchu jako: v = 2*pi*r/T. Wrzucając to do powyższego wzoru na promień otrzymujemy wzór na okres: T = 2*pi*m/qB. Widzimy zatem, że jeśli proton wpada pod jakimś określonym kątem, to niezależnie od wartości jego prędkości okres jest już ściśle określony, a wpadając pod jakimś określonym kątem zakreśla on określony fragment okręgu, toteż określony jest też czas jego przebywania w polu. A zatem czas ten nie zależy od wartości prędkości. Jeśli zmienimy kąt, to oczywiście zmieni się fragment okręgu zakreślany przez proton, a zatem zmieni się też czas przebywania protonu w polu i widzimy z powyższego wzoru na okres, że ów czas jest również zależny od stosunku q/m, stąd odpowiedzi to F,P,P.

9.4: siła wypadkowa musi być zerowa - zgodnie z drugą zasadą dynamiki, jeśli siłą ta będzie niezerowa, to proton będzie miał jakieś przyspieszenie, co będzie skutkowało zmianą jego kierunku ruchu (nawet jeśli to przyspieszenie byłoby wzdłuż jego kierunku ruchu, to zmieni się wtedy wartość prędkości protonu i wówczas siła Lorentza spowoduje już to zakrzywienie). A zatem wektor siły elektrycznej (którego zwrot jest faktycznie taki jak zwrot wektora E) musi być przeciwny do wektora siły Lorentza. I tak jest na rysunku IV, bowiem na rysunku IV wektor siły Lorentza nie jest zwrócony w prawo, ale pod kątem 45 stopni do granicy pola magnetycznego w prawy dół (jest prostopadła do wektora prędkości, zwrócona do środka okręgu, po którym teraz porusza się proton).