KeyserSoze 512 wyśw.
11-03-2022 23:13
Zadanie z matury próbnej - trygonometria
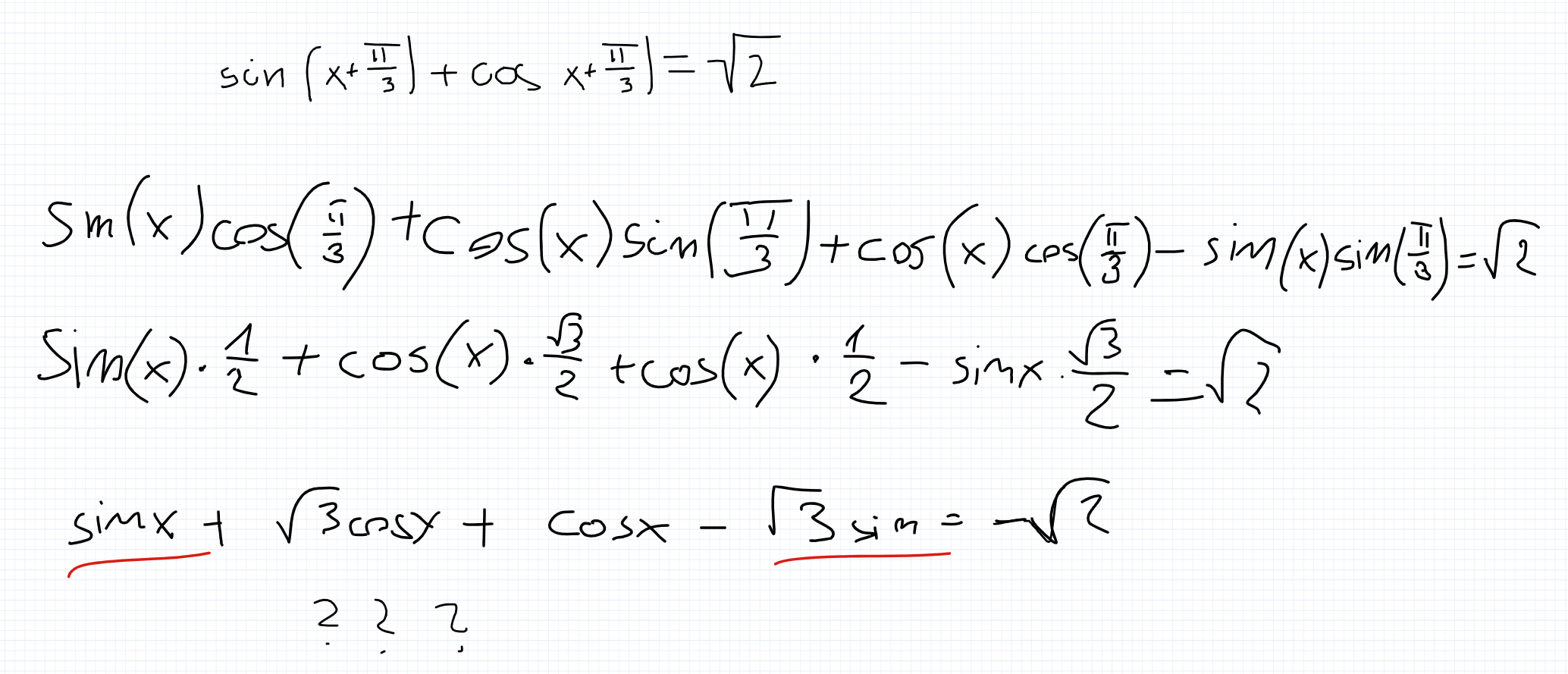
Doszedłem do momentu który widać w załączonym pliku, i się zaciąłem.
matematyka trygonometria Dodaj post do ulubionych Poproś o pomoc
Kliknij tutaj, aby dodać nowy komentarz.
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
qwerty4321
12-03-2022 11:15
- 2
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Felipe
12-03-2022 11:17
Polecam przekształcić początkowe równanie wzorami redukcyjnymi do sumy sinusów i zastosować wzór na tak ową sumę. Powinno wszystko wyjść;)
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Felipe
12-03-2022 11:17
viGor
12-03-2022 11:29
Można bez podnoszenia do kwadratu, unikniemy wtedy układu równań :)
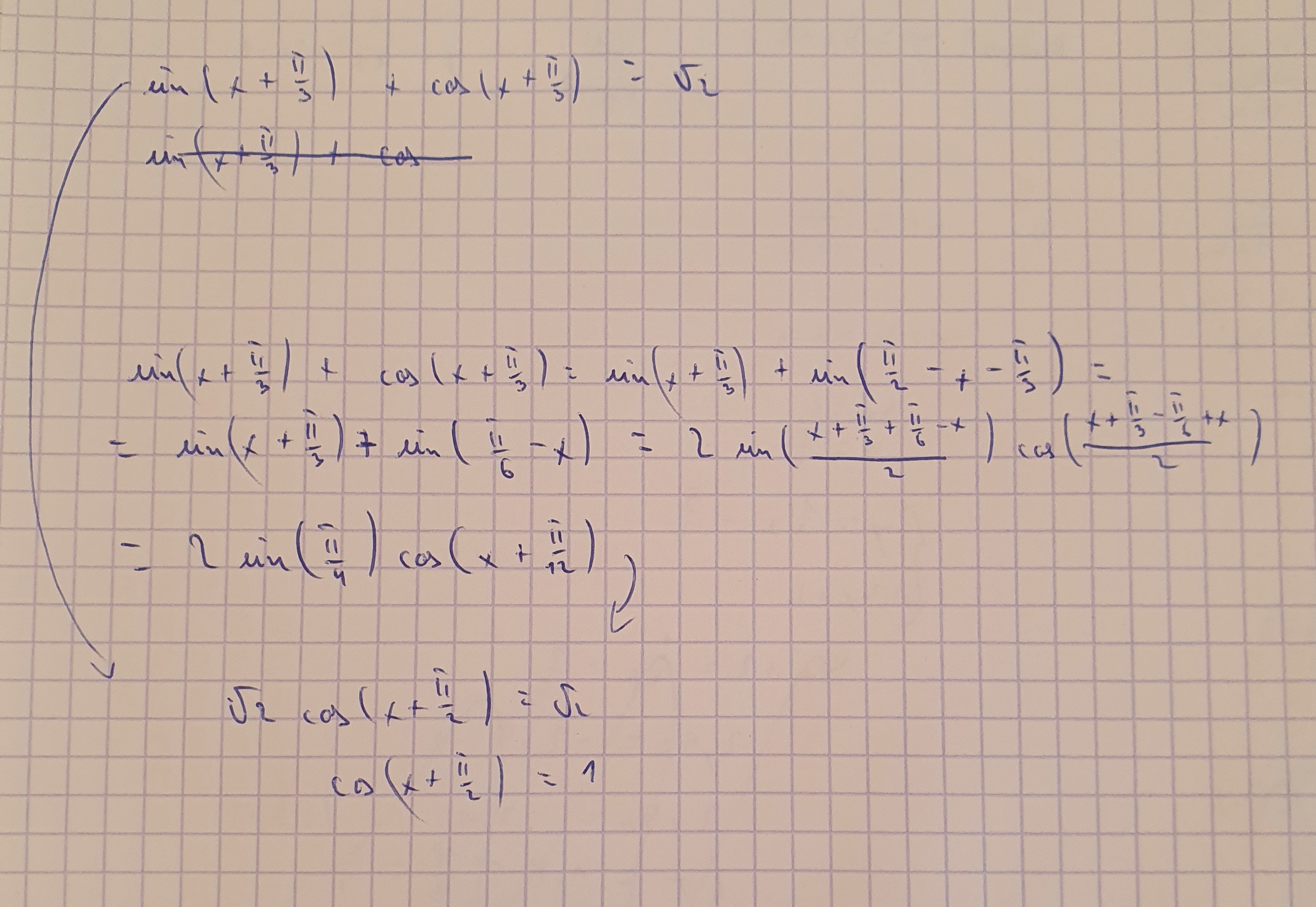
- 3
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
W przedostatnim wierszu jak pomnozyles razy dwa to nie pomnozyles prawej strony.
Ja bym to zadanie zrobil troche inaczej. Dla ulatwienia zapisu oznacze a = x + pi/3 .
sin(a) + cos(a) = sqrt(2) / do kwadratu
sin^2(a) + cos^2(a) + 2sin(a)cos(a) = 2 ,jedynka tryg
1 + 2sin(a)cos(a) = 2
sin(a)cos(a) = 1/2 / znowu do kwadratu
sin^2(a)*cos^2(a) = 1/4 ,cos^2(a) = 1 - sin^2(a)
rownanie stopnia czwartego, zmienna pomocnicza np. t = sin^2(a) i t nalezy do <0;1>. Delta itd.