Zad. 4a str. 96
Moje pytanie dotyczy tej nierówności: P(A) + P(B) - P(A iloczyn B) <= 1. Była ona podana w odpowiedziać i faktycznie doprowadza do tezy, ale czemu odejmujemy tam od P(A) i P(B) ich czesc wspolną? Bo generalnie rozumiem, że z aksjomatów prawd. tak wynika, ale czy ktos moglby mi to jakos lepiej wytlumaczyc? 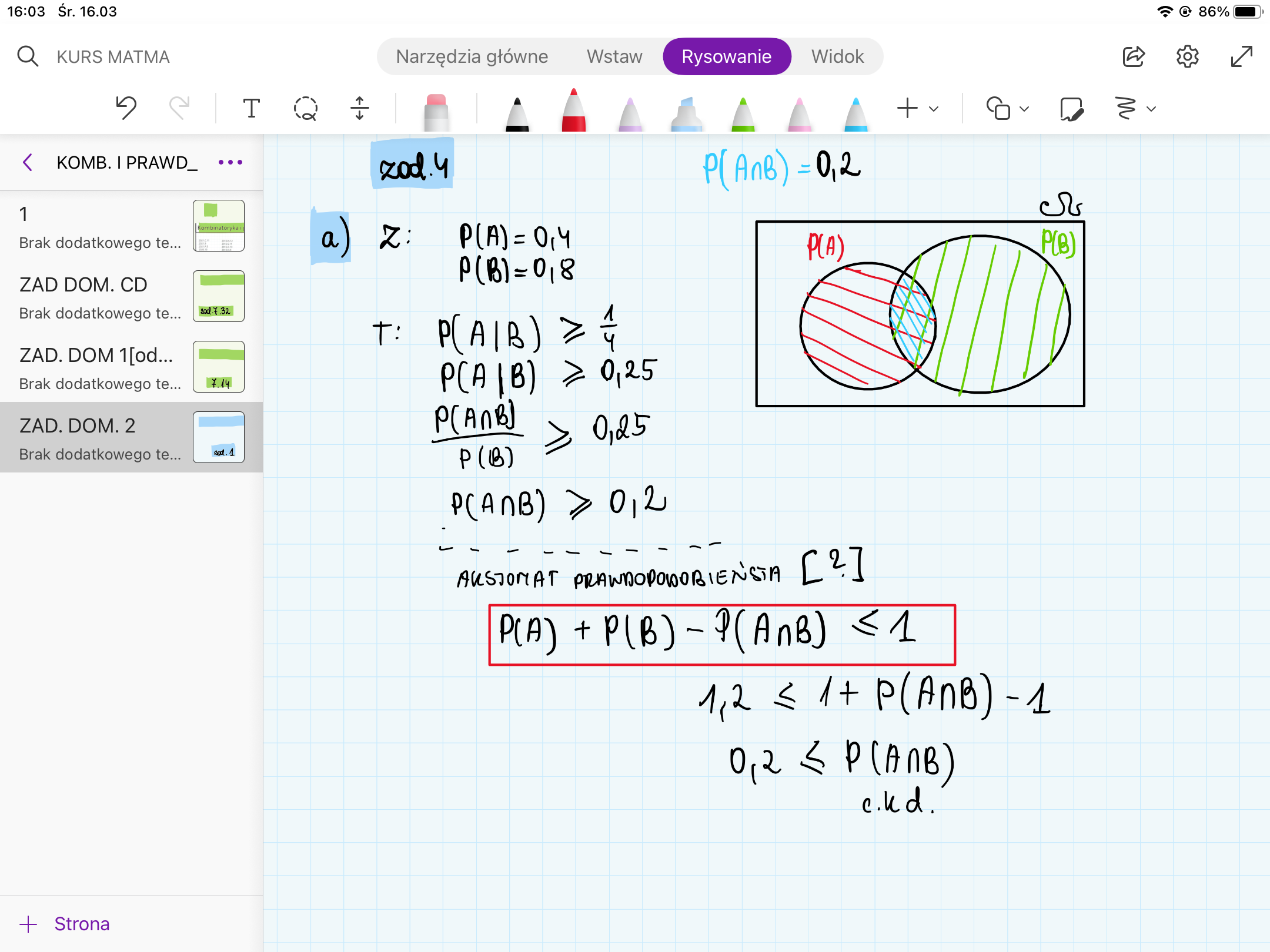
działania ja zbiorach Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
rozumiem. Bardzo dziękuję za pomoc <3
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
a tylko jeszcze jedno pytanko - skąd wiemy, że zbiory mają część wspólną? Tzn ja tak narysowałam, ale szczerze to nie wiedząc czy mają część wspólną. Chyba, że to wynika z tego, że suma P(A) i P(B) jest większa od jeden?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Nie musimy wiedzieć czy mają, jeśli nie mają to wtedy iloczyn zdarzeń AiB jest zbiorem pustym, więc wzór nadal działa - od P(A) + P(B) odejmiemy nic, więc się zgadza :)
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Aa no tak, racja, dziękuję raz jeszcze!
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Weźmy liczby, na nich będzie łatwo to pokazać. Wyobraź sobie, że masz zliczyć ile jest n-cyfrowych(dałem n, bo nie ma to znaczenia tutaj) liczb podzielnych przez 2 lub przez 3.
Jeśli policzymy ile jest parzystych, i dodamy do tego ilość liczb podzielnych przez , to wyjdzie nam za dużo, ponieważ niektóre liczby są podzielne przez 3 i przez 2[np. 6,12,30 itd.], dlatego od sumy liczb podzielnych przez 2 i liczb podzielnych przez 3, musimy odjąć ilość liczb podzielnych przez 6, wtedy mamy gwarancję, że każda liczba została policzona raz.
Podzielność liczb to tylko przykład, ale generalnie chcąc zrobić sumę zbiorów, to jeśli mają część wspólną(czyli w naszym przykładzie zbiór liczb podzielnych przez 3 i przez 2) należy ją odjąć.
Myślę, że w miarę dokładnie to wytłumaczyłem, daj znać czy już rozumiesz, a jeśli nie to spróbuję jeszcze jakiś inny przykład wymyślić, aby to pokazać :)