zadania optymalizacyjne

Niekoniecznie błąd, ja bym wrzucił x pod pierwiastek => pierwiastek(6x^2-x^3)/2, z tego wyznaczył f(x) - to, co znajduje się pod pierwiastkiem, następnie pochodną funkcji f(x) itd.

Czyli nie zwracać uwagi na mianownik? ( przy wyznaczeniu funkcji f(x)). I po zrobieniu tego będę nadal miał szukać np. Max czy się to zmienia i trzeba znaleźć Min?

robiąc zadanie z optymalizacji ułożyłem funkcję optymalizowaną z pierwiastkiem. Włożyłem wszystko pod pierwaistek i otrzymałem funkcję W(x) = pierwiastek (500 a^2 - a^4) / 2. Jako nową funkcję f(x) przyjąłem tylko (500 a^2 - a^4) które zoptymalizowałem, nic nie robiłem z mianownikiem i ostatecznie wyszedł mi dobry wynik. Czy takie coś się zawsze robi ? ( mianownik zostawia się gdy jest pierwiastek?)

Jakbyś wstawił konkretny przykład to byłoby prościej ocenić czy twoje rozwiązanie jest poprawne. Natomiast ogólnie, jeżeli mamy pierwiastek, to tak jak napisał @Kos. Oznaczamy funkcję podpierwiastkową jako g(x) i rozwiązujemy dla funkcji podpierwiastkowej. Pierwiastek jest funkcją rosnącą zatem jeżeli funkcja podpierwiastkowa dla pewnego "x" osiąga minimum/maximum, to funkcja cała również dla tego "x" osiągnie minimum/maximum.

A następnie postępujemy tak jak zawsze :)

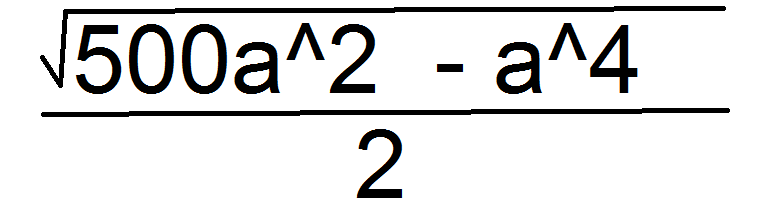
Zawsze optymalizujemy tylko to co jest pod pierwiastkiem? Mi chodzi o sytuację jak na zdjęciu. Czy jako f(x) bierzemy tylko pierwiastek czy mianownik też?

W tym przypadku. Stosujemy taki tok rozumowania:

Mianownik jest niezależną liczbą, zatem jeżeli wyznaczymy "a" dla którego licznik jest max/min. To dla takiego "a" całe wyrażenie będzie max/min. Ponieważ zajmujemy się tylko licznikiem, to wystarczy zająć się tylko tym co jest pod pierwiastkiem (wynika to z mojego poprzedniego komentarza). Zatem w tym przypadku wystarczy zbadać taką funkcję: g(x)=500a^2-a^4

Dziękuję bardzo