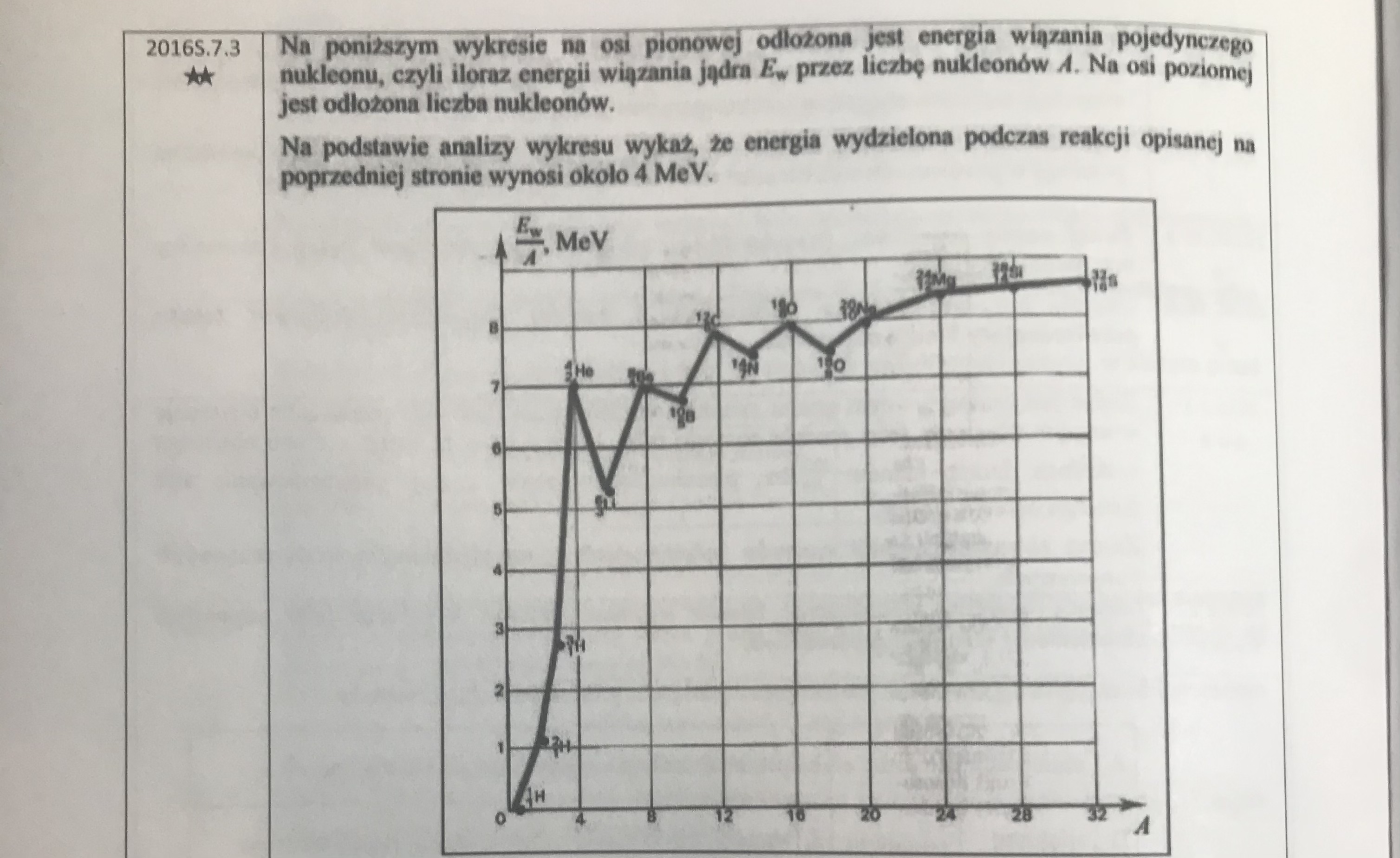
2016S.7.3

W takiej sytuacji zawsze najlepiej jest skorzystać po prostu z zasady zachowania energii całkowitej. Czyli: $$ E_{spocz,s} + E_{k,s} = E_{spocz,p} + E_{k,p} $$ Możemy założyć, że energia kinetyczna substratów była zerowa, a zatem to co chcemy obliczyć to energia kinetyczna produktów (to jest ta energia wydzielona). A zatem: $$ 2 m_{H2} c^2 = m_{H3} c^2 + m_p c^2 + E_{kp} $$ I teraz masy obu jąder (H-2 i H-3) możemy zgodnie z bilansem masy jądra zapisać jako sumy mas nukleonów minus deficyt masy. Zatem: $$ 2 (m_p + m_n - \delta m_{H2}) c^2 = (m_p + 2 m_n - \delta m_{H3}) c^2 + m_p c^2 + E_{kp} $$ Zauważmy, że te wszystkie masy protonów i neutronów się skrócą, a deficyt masy przemnożony przez c^2 to po prostu odpowiednia energia wiązania danego jądra, a zatem dostaniemy ostatecznie: $$ E_{kp} = E_{wiąz,H3} - 2 E_{wiąz,H2} $$