Zad 6 str 130

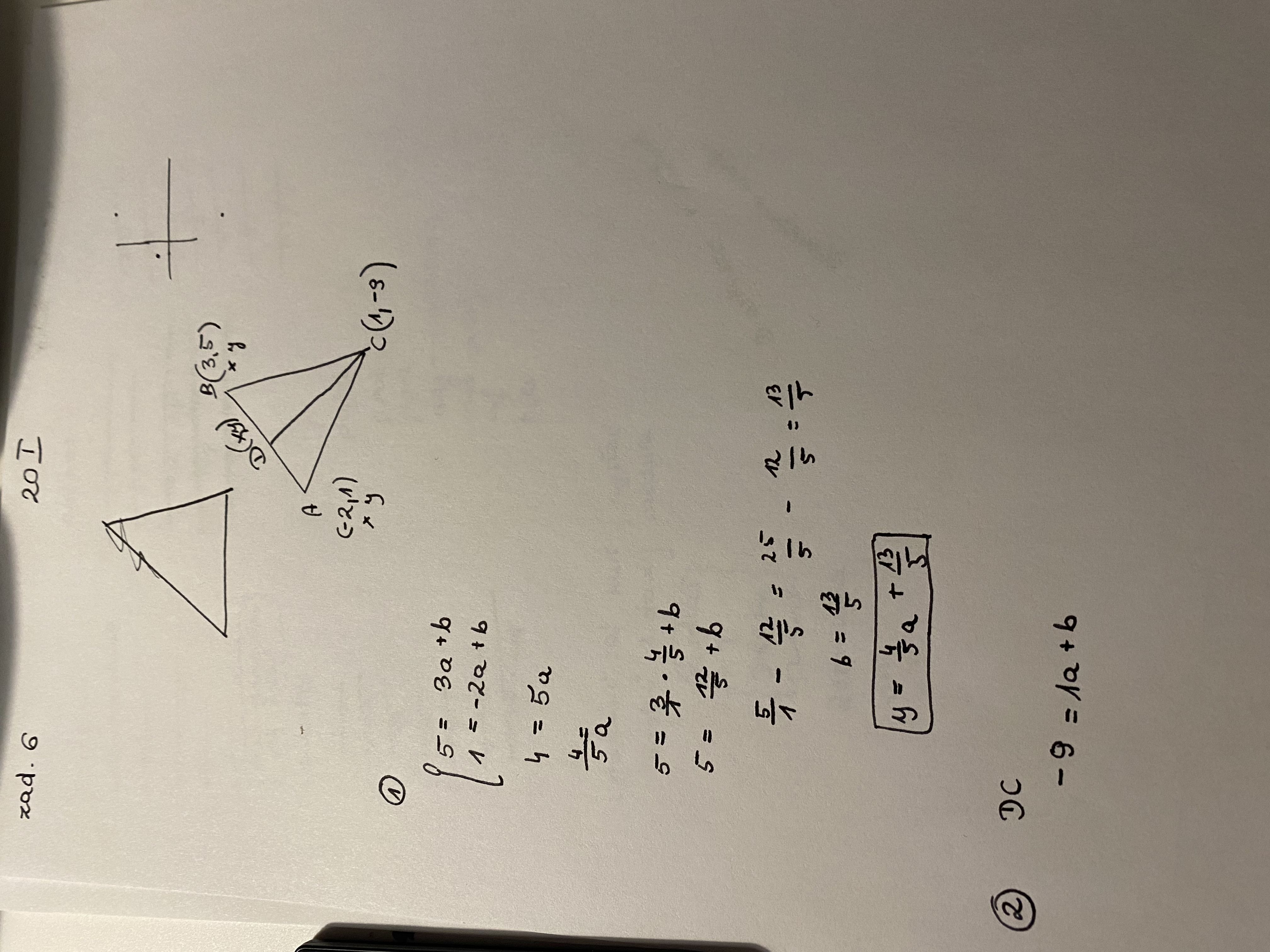
Masz już funkcje przechodzącą przez A, B
następnym krokiem będzie wyznaczenie współrzędnych punktu D.

wiemy, że CD jest wysokością, wysokość zawsze jest pod kątem prostym, czyli prosta AB jest prostopadła do prostej DC, w tym przypadku możemy wykorzystać własność a1*a2=-1, w tym przypadku współczynnik kierunkowy a prostej DC będzie a=-5/4

y=-5/4x+b <---- wzór funkcji zawierającej CD, by obliczyć "b" wystarczy podstawić tutaj punkt C, który znamy.

Kolejnym krokiem będzie wyznaczenie punktu D. Gdy już wyznaczymy funkcje zawierajaca punkt CD oraz AB wystarczy podstawić je do układu równań, z niego otrzymamy współrzędną x oraz y punktu D.

Ostatecznie wyznaczamy prostą przechodzącą przez BC (by poznac "a"), y=ax+b. By prosta przechodząca przez punkt D była równoległa do prostej przechodzacej przez BC to ich współczynniki kierunkowe muszą byc takie same a1=a2. otrzymamy wtedy prostą równoległą do prostej BC, ostatecznym krokiem będzie podstawienie punktu D od tej prostej i wyliczenie "b". To wszystko